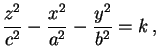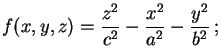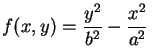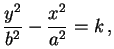|
|
A família a um parâmetro dos hiperbolóides de equação
com k variando de - a + infinito, forma a família das superfícies de nível da função real de três variáveis reais definida por
|
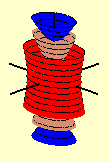
para cada k < 0 temos um hiperbolóide elíptico de uma folha de cor vermelha e, para cada k > 0, temos um hiperbolóide elíptico de duas folhas de cor azul; para um único parâmetro, k = 0, temos o cone elíptico de cor marrom. Na figura acima aparecem uma de cada um dos três tipos de superfície de nível.
Podemos ver o parâmetro k agindo temporalmente, animando a passagem de k dos negativos aos positivos. Visualizando os hiperbolóide dados pelos níveis k não com três deles simultaneamente como acima, mas sim um de cada vez, obtemos uma interpretação cinemática da família a um parâmetro de hiperbolóides. Como esta imagem animada é um pouco grande, ela pode ser melhor conferida em separado.
|
Concluímos esta página visualizando o análogo bidimensional desta família de hiperbolóides que é obtido através de um corte vertical: a função real passa a ser de duas variáveis reais, dada por
e as curvas de nível passam a ser as hipérboles dadas por
com k variando de - ¥ a + ¥. Nas figuras ao lado tomamos os parâmetros a2 = 1 e b2 = 1/2, mantivemos a cor vermelha para cada -100 < k < 0 e a cor azul para cada 0 < k < 350 ; para o único parâmetro k = 0, aparece um par de retas de cor marrom. Observe que a primeira figura à direita é o mapa de contornos do parabolóide hiperbólico. |
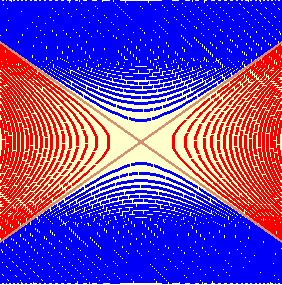
A Família Estática das Hipérboles 
A Família Cinemática das Hipérboles |