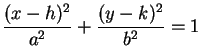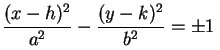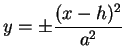Um cilindro quádrico é o lugar geométrico tridimensional de uma equação de segundo grau em duas variáveis, ou então, o que é mesma coisa, de uma equação de segundo grau em três variáveis em que uma das variáveis não aparece explicitamente.
Observe, para exemplificar, que a mesma equação x = 1 representa um ponto na reta unidimensional, uma reta vertical no plano bidimensional e um plano vertical no espaço tridimensional. Analogamente, uma equação

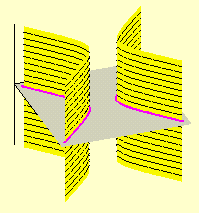
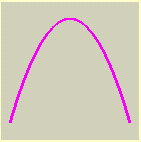
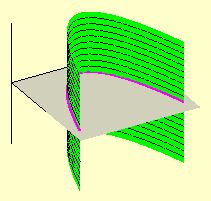
de segundo grau nas duas variáveis x e y, representa tanto uma cônica no plano x y quanto um cilindro quádrico no espaço tridimensional x y z. Nenhum valor da variável z (que não aparece na equação) deixa de satisfazer a equação e, assim, fazem parte do cilindro quádrico todas as retas verticais perpendiculares ao plano x y, sempre que o pé da perpendicular satisfaz a equação de duas variáveis dada. Utilizando a classificação das cônicas do Cálculo IA obtemos, entre outros, os cilindros elípticos, hiperbólicos e parabólicos, que podem ser visualizados a seguir; também apresentamos um cilindro obtido de uma cônica degenerada, mais precisamente, de um par de retas concorrentes. Estas quádricas são todas degeneradas, em termos da classificação dada acima.