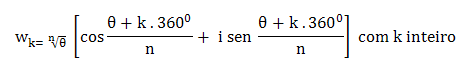NÚMEROS COMPLEXOS NA FORMA TRIGONOMÉTRICA
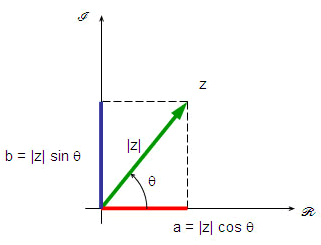
Na representação trigonométrica, um número complexo z = a + bi é determinado pelo módulo do vetor que o representa e pelo ângulo que faz com o semi-eixo positivo das abscissas.
Vetor é uma entidade matemática que define grandezas que
se caracterizam por módulo, direção e sentido, como
por exemplo, velocidade e força.
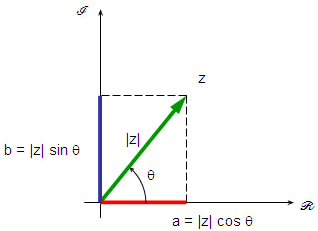
Um vetor é representado por um segmento de reta orientado. O módulo
é expresso pelo comprimento do segmento, a direção
é dada pelo ângulo entre a reta suporte e a horizontal, o
sentido é dado pela seta.
Denomina-se de afixo do complexo z = a + bi o ponto de
coordenadas (a, b) no plano complexo, denominado plano de Argand-Gauss.
Quando z = a+bi:

A partir das relações trigonométricas¹ obtêm-se:

A representação trigonométrica²
de um complexo z é argumento geral cálculo das raízes de z. |
| APLICATIVO 1 Este aplicativo
é em português e permite a visualização
de diferentes exemplos para a transformação de complexos
da forma algébrica para a trigonométrica e vice versa.
É essencial para o entendimento. |
Exemplos:
1. Se z é um número real, o ponto P pertence à reta
das abscissas (horizontal) e |z| = 1
Isto é: ![]() = 0+
k360° e |z| =1
= 0+
k360° e |z| =1
z = 1 na forma trigonométrica é z = cos k360°+ i sen
k360°, com k inteiro.
Isto quer dizer que existem muitas representações trigonométricas
para z, correspondentes a giros dados em torno da origem.
Neste caso, z = 1 pode ser representado por:
z = cos 0°+ i sen 0°
z = cos 360°+ i sen 360°
z = cos 720°+ i sen 720°
z = cos 1080°+ i sen 1080°
etc.
2. Se z é um número imaginário, o ponto P pertence
à reta das ordenadas (vertical) e |z| = 1
Isto é: ![]() = 90°+
k360° e |z| = 1
= 90°+
k360° e |z| = 1
z = i na forma trigonométrica é z = (cos (90°+k360°)+
i sen (90° +k360°)) com k inteiro.
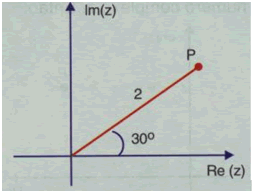
Na figura, OP representa um vetor e pode ser identificado com um número
complexo z.
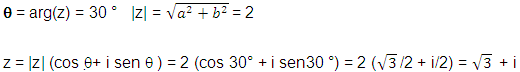
3 . O complexo z = 1 + i é representado na figura abaixo com:
a=1 e b=1 logo tg ![]() =
b/a = 1
=
b/a = 1
Então ![]() = 45°
= 45°
Este valor corresponde à menor determinação de ![]() :
-180°<
:
-180°< ![]() < 180°
< 180°
De uma forma geral ![]() = 45° + k360° , onde k é qualquer número inteiro
(positivo, negativo ou nulo) ou seja, o mesmo ângulo é obtido
a partir de um número inteiro de voltas em torno da origem O. Cada
volta corresponde a 360°.
= 45° + k360° , onde k é qualquer número inteiro
(positivo, negativo ou nulo) ou seja, o mesmo ângulo é obtido
a partir de um número inteiro de voltas em torno da origem O. Cada
volta corresponde a 360°.
O módulo r = ![]()
z = 1+i = r (cos ![]() +
i sen
+
i sen ![]() ) =
) = ![]() (
cos 45º+ i sen 45°)
(
cos 45º+ i sen 45°)
Esta forma corresponde à menor determinação para
![]() .
.
Igualdade de Números Complexos
Dados dois complexos z = a + i b e w = c + i d tem-se:
z = r (cos (![]() + k.360°)+
i sen (
+ k.360°)+
i sen (![]() + k.360°))
+ k.360°))
w = r’ (cos (![]() +
k.360°)+ isen (
+
k.360°)+ isen (![]() +
k.360°))
+
k.360°))
z = w |
Observe que a igualdade exige que r = r’ mas não exige que
![]() =
= ![]() ,
mas, sim, que os vetores coincidam, na mesma direção, módulo
e sentido.
,
mas, sim, que os vetores coincidam, na mesma direção, módulo
e sentido.
Simétrico de um Número Complexo
O simétrico do número complexo z = a + ib é o número
-z = - (a + ib), ou seja,
-z = (-a) + i(-b).
Corresponde a uma rotação de 180º do afixo de z em
torno da origem.
Em notação trigonométrica:
z = r (cos |
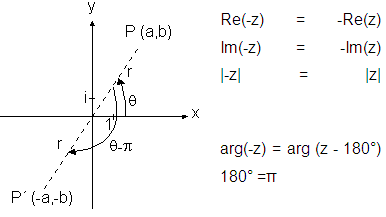
Exemplo:

Conjugado de um Número Complexo
O conjugado do complexo z = a + ib é o número
complexo denotado por
z = a - ib.
Na forma trigonométrica, o conjugado de
z = r (cos |
Corresponde a uma reflexão do afixo de z na reta
das abcissas
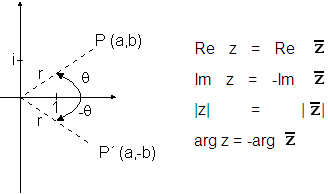
Exemplo:
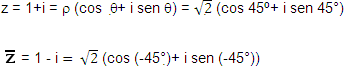
Inverso de um número complexo

Observe que:

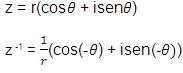 |
Exemplo:
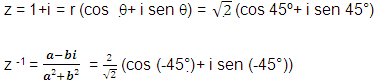
APLICATIVO 2 |
Produto de complexos
Seja z = r (cos![]() + i sen
+ i sen![]() )
e w = r’ (cos
)
e w = r’ (cos![]() + i
sen
+ i
sen![]() )
)
Vejamos a interpretação geométrica do produto de
dois complexos,
Caso 1: O produto de um complexo z por um número
real K
K.z = Kr (cos |
Se K > 1, então esta operação corresponde a uma
ampliação vetor z .
Se 0 < K < 1, esta operação corresponde a uma contração
do vetor z.
Se K < 0, esta operação corresponde a uma ampliação
ou contração, seguida de uma rotação de 180º,
pois z passará para a semi-reta oposta, que contém (-z).
Exemplo:
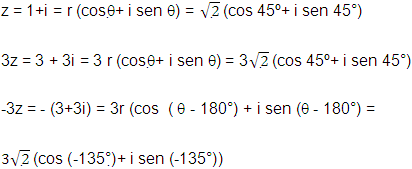
Caso 2: O produto de um complexo z = a + bi por um imaginário
puro.
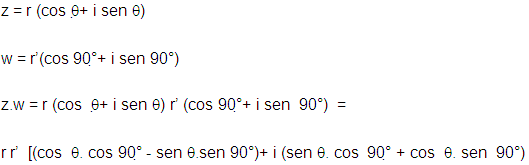
É preciso, neste momento, relembrar a expressão trigonométrica
para seno e cosseno da soma de arcos (ou ângulos)³
:

Logo

Voltando
|
Estas operações podem ser facilmente visualizadas na figura
seguinte:
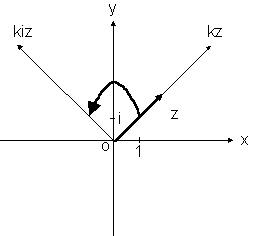
Caso 3: O produto de um complexo genérico z
por outro complexo w

|
|
Observe, na figura: o vetor tem módulo r e argumento ![]() :
:
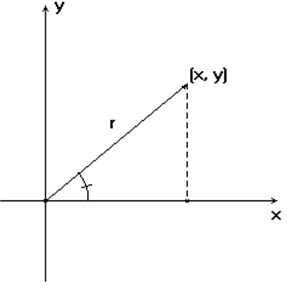
Ao ser multiplicado por outro vetor com ângulo ![]() ,
ele gira, sofre uma rotação de ângulo
,
ele gira, sofre uma rotação de ângulo ![]() :
:
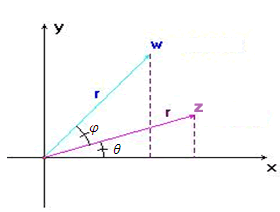
Potenciação com expoente inteiro
Vamos nos restringir à potências com expoente inteiro,
embora, nos complexos seja possível definir potência com
base e expoente complexo.
Chamamos potenciação a uma potência de expoente
inteiro.
![]()
z = r (cos![]() + i sen
+ i sen![]() )
)
Como o produto de dois complexos corresponde à soma dos argumentos,
temos:
z² = r²(cos (2![]() )+
i sen (2
)+
i sen (2![]() ))
))
z³ = r³(cos (3![]() )+
i sen (3
)+
i sen (3![]() ))
))
A demonstração da Fórmula de Moivre pode ser vista na Apresentaçao: potênciação e radiciação
APLICATIVO 3
http://www.drec.min-edu.pt/Eviprof/resources/school7/files/trab2/complejos5.htm |
|
APLICATIVO 4
http://www.drec.min-edu.pt/Eviprof/resources/school7/files/trab2/complejos6.htm |
|
Dado z, complexo, chamamos raiz n-ésima de z, a todo
w complexo tal que |
Exemplos:
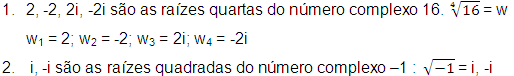
|
A pergunta então é: quantas são as raízes
enésimas de um número complexo |
|
Pelo Teorema Fundamental da Álgebra,a equação
complexa |
Sendo z = r (cos![]() +
i sen
+
i sen![]() ) as raízes
índice n de z são dadas pela fórmula de de Moivre.
) as raízes
índice n de z são dadas pela fórmula de de Moivre.
Na Apresentação:
Potenciação e Radiciação,
você encontra a demonstração.
Veja o exemplo da equação ![]() na Apresentação:
Raízes da Unidade
na Apresentação:
Raízes da Unidade
|
APLICATIVO 5
É essencial que você manipule este
aplicativo. Com ele, toda esta “complicação”
algébrica vai ficar clara: |
APLICATIVO 6
Neste aplicativo, você pode visualizar
a potenciação e a fórmula de Moivre. • Check "Show additional line".---
Peça para mostrar linhas adicionais, para ver polígonos.
Pressione Additional Line |
Este texto foi baseado em:
Números Complexos, uma Abordagem Científica extraído
do site http://www.educ.fc.ul.pt/docentes/opombo/seminario/euler/numeroscomplexos.htm#Representação%20Trigonométrica
CARMO, Manfredo; MORGADO, Augusto; WAGNER, Eduardo. Trigonometria e Números Complexos. Publicação SBM, 2001, 122 p.
_________________________________________________________________________
Notas Finais
¹
Se você quiser relembrar as relações trigonométrica,
assista:
http://www.youtube.com/watch?v=FZLXujO3yw8
http://www.youtube.com/watch?v=YRt4Ni73954&NR=1
²
Se você quiser saber mais sobre a representação
trigonométrica de um complexo, veja:
http://pessoal.sercomtel.com.br/matematica/trigonom/trigo03.htm
³
Se você quiser verificar as justificativas destas expressões,
veja em:
http://criar.no.sapo.pt/sen_cos.html