Resposta do Exercício 3

Retas Simétricas em relação ao eixo OX

Em primeiro lugar, precisamos entender o que significa dizer que dois gráficos são simétricos em relação ao eixo OX.
Podemos começar analizando apenas dois pontos.
Dois pontos são simétricos em relação ao eixo OX quando um é a reflexão do outro em relação a esse eixo, ou, analizando de outra maneira, quando possuem mesma abscissa e ordenada simétrica.
Por exemplo, o simétrico do ponto (2,1) em relação do eixo OX é o ponto (2,-1).
O mesmo acontece com os pontos dos gráficos em questão: um ponto do gráfico g(x) = 2x + 4 é (x, 2x+4) e seu simétrico em relação ao eixo OX é (x, -(2x+4)).
A função que tem como ponto (x, -(2x+4)) é f(x) = -(2x+4) = -2x - 4, ou seja, os valores de "a" e "b" para que as retas g(x)= 2x + 4 e f(x)= ax + b sejam simétricas em relação ao eixo OX são:

a = -2
b = -4

Veja os gráficos.

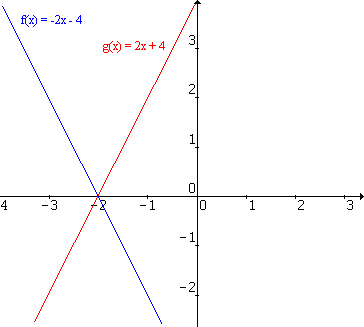Retas Simétricas em relação ao eixo OY

Em primeiro lugar, precisamos entender o que significa dizer que dois gráficos são simétricos em relação ao eixo OY.
Podemos começar analizando apenas dois pontos.
Dois pontos são simétricos em relação ao eixo OY quando um é a reflexão do outro em relação a esse eixo, ou, analizando de outra maneira, quando possuem mesma ordenada e abscissa simétrica.
Por exemplo, o simétrico do ponto (3,5) em relação do eixo OX é o ponto (-3,5).
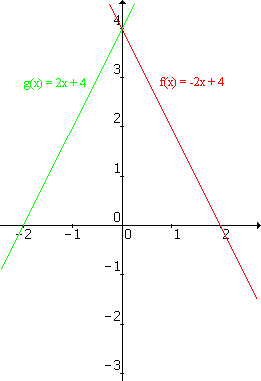
O mesmo acontece com os pontos dos gráficos em questão: um ponto do gráfico g(x)= 2x + 4 é (x, 2x+4) e seu simétrico em relação ao eixo OY é (-x, 2x+4).
A função que tem como ponto (-x, 2x+4) é f(x)= 2(-x) + 4 = -2x + 4, ou seja, os valores de "a" e "b" para que as retas g(x)= 2x + 4 e f(x)= ax + b sejam simétricas em relação ao eixo OY são:

a = -2
b = 4

Veja os gráficos.

Retas Simétricas em relação à reta y = x

Vamos primeiro entender o que significa dizer que duas retas são simétricas em relação à reta y = x: duas retas são simétricas em relação à reta y = x quando uma é a reflexão da outra em relação a essa reta.
Vamos olhar para a figura ao lado: por congruência de triângulos, podemos concluir que a distância de O à x₁ é a mesma distância de O à y₂ e que a distância de O à x₂ é a mesma distância de O à y₁. Como o ponto (x₁, y₁) pertence à reta g(x)= 2x + 4 e o ponto (x₂,y₂) pertence à reta f(x)= ax + b e o valor de x₁ equivale ao valor de y₂ assim como o valor de x₂ equivale ao valor de y₁, faremos a seguinte álgebra:
g(x) = 2x + 4
y₁ = 2x₁ + 4
x₂ = 2y₂ + 4
y₂ = (x₂ - 4)/2
y₂ = x₂/2 - 2
f(x) = x/2 - 2
Logo, os valores de "a" e "b" para que as retas g(x)= 2x + 4 e f(x)= ax + b sejam simétricas em relação à reta
y = x são:

a = 1/2
b = -2

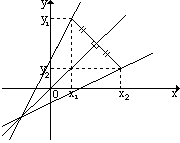Obs: Funções que são simétricas em relação à reta y = x são chamadas também de Funções Inversas.

Retas Paralelas

Retas paralelas nada mais são que retas transladadas, já visto no segundo exercício. O parâmetro "a" permanece constante, pois não queremos alterar a inclinação da reta e o parâmetro "b" pode assumir qualquer valor. Enfim, os valores de "a" e "b" para que as retas g(x)= 2x + 4 e f(x)= ax + b sejam paralelas são:

a = 2
b qualquer

Logo, f(x) = 2x + b

Retas Perpendiculares

Para resolvermos este problema, vamos considerar duas retas perpendiculares que passam pela origem do sistema, como mostra o desenho ao lado. Olhando para o desenho, percebemos que os dois triângulos destacados são semelhantes, pois possuem os três ângulos congruentes (faça essa dedução). Como os triângulos são semelhantes, seus lados são proporcionais. Daí, tiramos a proporção abaixo:

Como o coeficiente angular (inclinação) de uma reta que passa pela origem é dada por "y/x", podemos concluir que o coeficiente angular de duas retas perpendiculares são "inversos e simétricos".
Logo, os valores de "a" e "b" que tornam as retas g(x)= 2x + 4 e f(x)= ax + b perpendiculares são:

a = -1/2
b qualquer

Então, f(x) = -1/2x + b

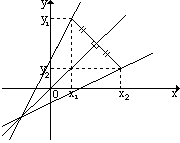
Volta para Movimentos sobre Gráficos