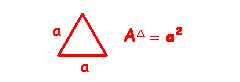TRABALHANDO COM A UNIDADE DE ÁREA TRIANGULAR
Daniela Stevanin Hoffmann *
Maria Alice Gravina *
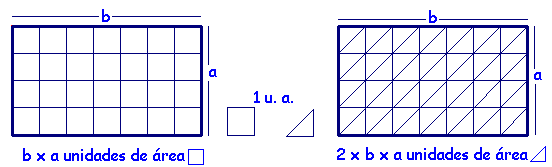
A área de uma figura plana mostra o quanto ela ocupa de lugar no plano, e como vimos, pode ser medida por comparação com uma unidade de área pré-determinada, contando quantas unidades de área "cabem" na figura.
Normalmente, adota-se um quadrado como unidade de área, mas e se adotássemos um triângulo?
Na figura abaixo, medimos a área de um retângulo de duas formas diferentes: primeiro contamos quantos quadrados unidades de área existiam no retângulo; depois contamos quantos triângulos retângulos unidades de área existiam no retângulo e...
obtivemos números diferentes!!!
Pode o mesmo polígono ter duas áreas diferentes?
SIM!!
Depende da unidade de área adotada!
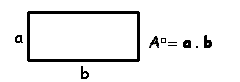
As fórmulas de áreas que estudamos estão todas fundamentadas na escolha da unidade de área quadrada. Tal unidade nada mais é que um quadrado de lado 1 unidade de comprimento que convencionamos ter área 1 unidade de área. Com esta unidade temos:
... etc.
Mas e se utilizássemos outras figuras como unidade de área, por exemplo, retângulos, triângulos, círculos, hexágonos, etc?
Como ficariam as fórmulas de área de figuras bem conhecidas nessas outras unidades?
 
O TRIÂNGULO EQUILÁTERO COMO UNIDADE DE ÁREA E
CORRESPONDENTES FÓRMULAS DE ÁREA DE ALGUNS POLÍGONOS
No que segue, vamos tomar como unidade de área - - um triângulo equilátero de lado 1 u.c. o qual convencionamos ter área igual a 1 u.a.
 

Cálculo da Área de um Triângulo Equilátero em unidades

Vamos agora deduzir que a fórmula da área de um triângulo equilátero A com lado de comprimento a, em unidades , é ccccccccccccccccccccccccc .
De fato, acompanhando a figura, vemos que se:
, , , ,
logo, para um triângulo equilátero de lado a, a área é dada pelo total de triângulos unidade que o compõe. Continuando o procedimento de contagem feito acima, temos que, a fórmula da área de um triângulo equilátero de lado a é dada pela soma dos números ímpares. Isto nada mais é que a soma dos termos de uma Progressão Aritmética (PA) com o primeiro termo igual a 1 e a razão igual a 2. Usando a fórmula da soma dos termos de uma PA, temos:
Assim podemos afirmar que para um triângulo equilátero de medida inteira, a fórmula da sua área,
em unidades , é ccccccccccccccccccccccccc.
Tal fórmula pode ser generalizada para triângulos de lado de medida real.
 

Cálculo da Área de um Triângulo com um ângulo de 60º em unidades

Agora vamos mostrar que a fórmula da área de um triângulo com ângulo de 60º, em unidades , é
.

Como se sabe, a área de um triângulo qualquer pode se calculada, em unidades , pela fórmula , no caso do triângulo com ângulo de 60º, essa fórmula fica

.
Para converter essa fórmula dada em unidades para uma fórmula em unidades precisamos saber a relação que existe entre um unitário e um unitário, ou seja, sendo , quanto vale k. Assim, poderemos fazer a conversão de unidades para unidades através de .
Aplicando a fórmula do triângulo com ângulo de 60º, em unidades , ao nosso triângulo equilátero unitário temos que A, isto é, cada é igual a . .
Portanto, , ou ainda .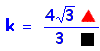
Agora, usando , k e , obtemos .
Assim, podemos afirmar que a área de um triângulo com ângulo de 60º é dada por, em unidades ,
.
Observe que essa mesma fórmula de cálculo de área pode ser utilizada em um triângulo com ângulo de 120º, já que o
sen 60º = sen 120º.
 

Observe que estes dois triângulos tem expressões de área bastante simples ( e ).
Se tomarmos estas expressões em unidades quadradas, elas correspondem às fórmulas das áreas do quadrado e do retângulo. Assim, podemos fazer um paralelo:
 

Como ficaria o Teorema de Pitágoras em unidades ?

Pitágoras construiu quadrados a partir de cada lado de um triângulo retângulo e mostrou que suas áreas são relacionadas, em unidades , por .
Veja uma ANIMAÇÃO JAVA do Teorema!
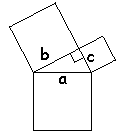
No contexto de unidade , vamos construir triângulos equiláteros a partir dos lados de um triângulo com ângulo de 60º ou 120º e mostrar que suas áreas estão relacionadas conforme mostra a tabela:
Faremos o Teorema de Pitágoras Triangular.
Observe que a recíproca também é verdadeira, isto é, se a expressão for verificada então o triângulo do meio (representado por ) será um triângulo com ângulo de 60º ou 120º.
 
Demonstração:
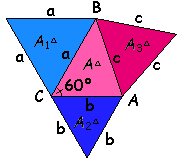
1º Caso:
Tomamos um triângulo com ângulo de 60º com lados de medidas a, b e c. Construímos um triângulo equilátero de lados a+b. Conforme mostra a figura abaixo, construímos três triângulos congruentes ao triângulo com ângulo de 60º em questão.
xxxxxxxxxxxxxxxxxxx
Assim, a área em unidades do triângulo equilátero de lados a+b é igual a soma das áreas dos triângulos que o formam:
assim,

vvvvv
Esta relação pode ser reinterpretada em termos de área:


2º Caso:
Por outro lado, se tomarmos um triângulo de 120º com lados medindo a, b e c, com ab, construímos um triângulo equilátero de lado . Conforme mostra a figura abaixo, construímos três triângulos congruentes ao triângulo com ângulo de 120º, um triângulo equilátero de lado c e três triângulos equiláteros de lado a.
bbbbbbbbbbbbbbb
Então, novamente, o triângulo equilátero de lado tem área, em unidades , dada pela soma das áreas dos triângulos que o formam:
portanto,

Esta relação pode ser reinterpretada em termos de área:

Assim, fica completa a demonstração do Teorema de Pitágoras Triangular.

Fica como um desafio para você, fazer a transformação de outras fórmulas de área de figuras conhecidas de unidades para unidades .
Como ficaria a fórmula de um quadrado, ou de um paralelogramo, ou de um retângulo, ou de um ... ?

Volta para ATIVIDADES


Inspirada no artigo: A triangular analogue of the Pytagorean theorem; The Mathematical Gazette, vol.80, nº489, nov. 1996.

Daniela Stevanin Hoffmann é licencianda em Matemática e bolsista da Prof. Maria Alice Gravina.
E-mail: dsh@mat.ufrgs.br 
Maria Alice Gravina é professora do curso de Licenciatura em Matemática da UFRGS, mestre em Matemática pelo IMPA-CNPq e aluna do programa de doutorado em Informática na Educação-UFRGS. 
E-mail:gravina@mat.ufrgs.br