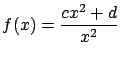Mat01353 - Cálculo e Geometria Analítica I-A
Primeira Verificação : Fila B - 2003/2
Veja aqui o gabarito em HTML (Explorer, Mozilla).
Veja aqui o gabarito em PDF (Acrobat Reader).

Questão 1. (1.5 pontos) Verifique se a função 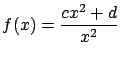$$f(x) = \frac{cx^2 + d}{x^2}$$, $c > 0$ e $d > 0$, possui assíntotas horizontais e/ou verticais. Justifique sua resposta. Em caso afirmativo, determine as equações de todas assíntotas.

Questão 2. (1.5 pontos) Considere a função $f(x) = 3 x^2 - 2 \ln(x)$.

(a) (1 ponto) Determine as abscissas de todos os pontos do gráfico de $f$ nos quais a reta tangente é paralela à reta $4x-y + 3 = 0$.

(b) (0.5 pontos) Considere $h(x) = \frac{f(x)}{g(x)}$, onde $f$ é dada acima e $g$ é uma função derivável em ${\mathbb{R}}$. Sabendo que $g(1) = 1/4$ e $g'(1) = 1/3$, determine $h'(1)$.

Questão 3. (1.5 pontos)

Determine $k$ de modo que a função $f$ seja contínua em $x=0$, onde

$$f(x) = \left\{ \begin{array}{lr} \displaystyle \frac{\mbox{sen} \... ...x}, & \mbox{se} x > 0 \\ x^2 - 3k , & \mbox{se} x \leq 0 \end{array} \right.$$

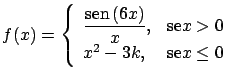
Questão 4. (2.0 pontos)

(1) (1.0 ponto) Usando a definição de derivada em um ponto,

$$f'(x_0) = \lim_{x \rightarrow x_0} \frac{f(x)-f(x_0)}{x-x_0}$$

determine $f'(x_0)$ para $x_0 = -3$, onde $f(x) = x^2 - 2x$.

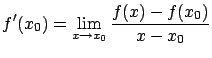
(2) (1.0 ponto) Considere a curva de equação $e^{2xy} - y^3 + 2x^2 = 9$. Determine:

(a) $$\frac{dy}{dx}$$ (b) a equação da reta tangente à curva no ponto $(2,0)$

Questão 5: (2.0 pontos) O gráfico de uma função $f$, definida em $[-1,3]$, é dado abaixo.

(a) Faça um esboço do gráfico da derivada de $f$.

(b) Faça um esboço do gráfico de $g(x) = 1 - f(x)$.

(c) Faça um esboço do gráfico de $h(x) = \vert 1 - f(x)\vert$.

Questão 6: (1.5 pontos) Um holofote está no solo a 20 m de um edifício. Um homem de 1.80 m de altura anda a 1.5 m/s, a partir do holofote em direção ao edifício.

(a) Expresse o comprimento $s$ da sombra do homem, sobre o edifício, em função de sua distância $x$ ao holofote. Indique o domínio da função .

(b) Determine a taxa de variação instantânea de $s$ em relação ao tempo quando o homem estiver a 17 m do edifício (indique a unidade). Neste instante, o comprimento da sobra está aumentando ou diminuindo ?

Justifique suas respostas.