Polinômios de Legendre - parte 2



O propósito aqui é dar prosseguimento à exposição da teoria dos polinômios de Legendre, iniciada na parte 1.

Fórmula de Recorrência.

$\displaystyle (n+1)\,P_{n+1}(x)-(2\,n+1)\,x\,P_n(x)+n\,P_{n-1}(x)=0 \ \ , \qquad n=1,2,3,\ldots $

Dem:

Na demonstração vamos novamente usar a função geradora.

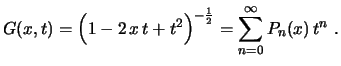
$\displaystyle G(x,t)=\Bigl(1-2\,x\,t+t^2\Bigr)^{-\frac{1}{2}}= \sum_{n=0}^\infty P_n(x)\,t^n \ . $

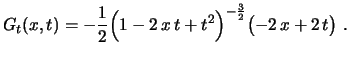
$\displaystyle G_t(x,t)=-\frac{1}{2}\bigl(1-2\,x\,t+t^2\bigr)^ {-\frac{3}{2}}\bigl(-2\,x+2\,t\bigr) \ . $

Logo

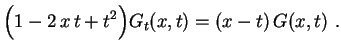
$\displaystyle \Bigl(1-2\,x\,t+t^2\Bigr)G_t(x,t)= (x-t)\,G(x,t) \ . $

Segue que

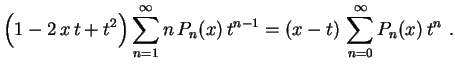
$\displaystyle \Bigl(1-2\,x\,t+t^2\Bigr)\sum_{n=1}^\infty n\,P_n(x)\,t^{n-1}=(x-t)\,\sum_{n=0}^\infty P_n(x)\,t^n \ . $

Multiplicando, obtém-se

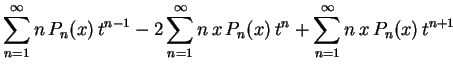
$\displaystyle \sum_{n=1}^\infty n\,P_n(x)\,t^{n-1}-2 \sum_{n=1}^\infty n\,x\,P_n(x)\,t^n+ \sum_{n=1}^\infty n\,x\,P_n(x)\,t^{n+1} \hspace{3.5cm} $


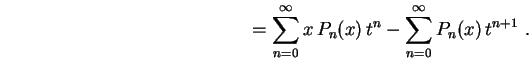
$\displaystyle \hspace{5.5cm} =\sum_{n=0}^\infty x\,P_n(x)\,t^n- \sum_{n=0}^\infty P_n(x)\,t^{n+1} \ . $

ou seja,

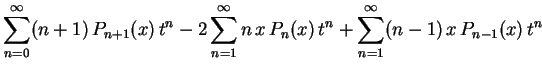
$\displaystyle \sum_{n=0}^\infty (n+1)\,P_{n+1}(x)\,t^n-2 \sum_{n=1}^\infty n\,x\,P_n(x)\,t^n+ \sum_{n=1}^\infty (n-1)\,x\,P_{n-1}(x)\,t^n \hspace{3.5cm} $


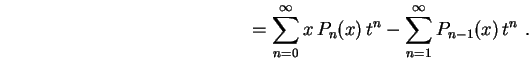
$\displaystyle \hspace{5.5cm} =\sum_{n=0}^\infty x\,P_n(x)\,t^n- \sum_{n=1}^\infty P_{n-1}(x)\,t^n \ . $

Agrupando os termos, obtemos, finalmente,

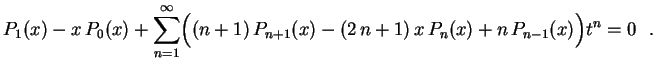
$\displaystyle P_1(x)-x\,P_0(x)+\sum_{n=1}^\infty\Bigl( (n+1)\,P_{n+1}(x)-(2\,n+1)\,x\,P_n(x)+n\,P_{n-1}(x) \Bigr)t^n=0 \ \ . $

Igualando a 0 o coeficiemte de cada $ t^n$ segue a conclusão.

Obs: Conhecendo 2 polinômios de Legendre consecutivos, a fórmula de recorrência nos permite calcular o próximo. Por exemplo, vimos acima que

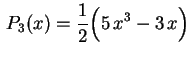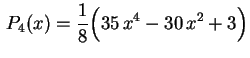$ \displaystyle\,P_3(x)=\frac{1}{2} \Bigl(5\,x^3-3\,x\Bigr)$         e         $ \displaystyle\,P_4(x)= \frac{1}{8}\Bigl(35\,x^4-30\,x^2+3\Bigr)$ .


Fazendo $ n=4$ na fórmula de recorrência, vamos obter

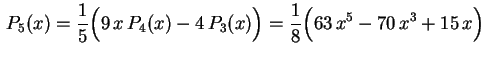$ \displaystyle\,P_5(x)=\frac{1}{5} \Bigl(9\,x\,P_4(x)-4\,P_3(x)\Bigr)=\frac{1}{8} \Bigl(63\,x^5-70\,x^3+15\,x\Bigr)$ .


Tendo agora as expressões de $ \,P_4(x)\,$ e $ \,P_5(x)\,$, usando novamente a fórmula de recorrência, podemos obter $ \,P_6(x)\,$, e assim por diante.

Desenvolvimento em Série de Fourier-Legendre.

Vimos na parte 1 que $ \,\{P_n(x)\}\,$ forma um sistema ortogonal no intervalo $ \,[-1,\,1]\,$. Usando este fato, dada uma função $ \,f:[-1,\,1]\longrightarrow\mathbb{R}\,$ de classe $ C^1$ por partes, vamos querer expandi-la como

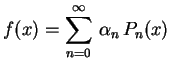$\displaystyle f(x)=\sum_{n=0}^\infty\,\alpha_n\,P_n(x)$    (série de Fourier-Legendre) .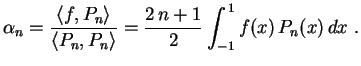$\displaystyle $

Como em qualquer expansão em série de funções ortogonais, os coeficientes são dados por

$\displaystyle \alpha_n=\frac{\langle f,P_n\rangle}{\langle P_n,P_n\rangle} =\frac{2\,n+1}{2}\int_{-1}^{\,1}f(x)\,P_n(x)\,dx \ . $



Exemplo: Expandir em série de Fourier-Legendre a função $ \,f:[-1,\,1]\longrightarrow\mathbb{R}\,$, $ \,f(x)=\lvert x\rvert\,$.

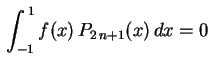Como $ \,f(x)\,$ é uma função par, $ \,\alpha_{2\,n+1}=0\,$, pois, sendo $ \,P_{2\,n+1}(x)\,$ ímpar e $ \,f(x)\,$ par, segue que $ \,f(x)\,P_{2\,n+1}(x)\,$ é ímpar e, portanto, $ \displaystyle\,\int_{-1}^{\,1}f(x)\, P_{2\,n+1}(x)\,dx=0\,\rule{0.cm}{0.7cm}$. Analogamente

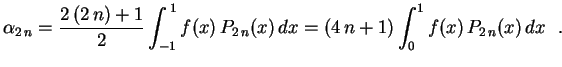
$\displaystyle \alpha_{2\,n}=\frac{2\,(2\,n)+1}{2}\int_{-1}^{\,1} f(x)\,P_{2\,n}(x)\,dx=(4\,n+1)\int_0^1 f(x)\,P_{2\,n}(x)\,dx \ \ . $

Mas da fórmula de recorrência segue que

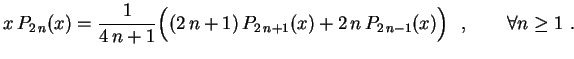
$\displaystyle x\,P_{2\,n}(x)=\frac{1}{4\,n+1}\Bigl( (2\,n+1)\, P_{2\,n+1}(x)+2\,n\,P_{2\,n-1}(x)\Bigr) \ \ , \qquad \forall n \geq 1 \ . $

Integrando, temos

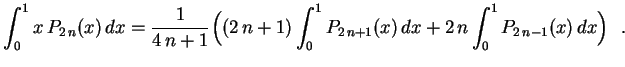
$\displaystyle \int_0^1x\,P_{2\,n}(x)\,dx=\frac{1}{4\,n+1}\Bigl( (2\,n+1)\int_0^1P_{2\,n+1}(x)\,dx+ 2\,n\int_0^1P_{2\,n-1}(x)\,dx\Bigr) \ \ . $

Mas acima, como aplicação da função geradora, obtivemos

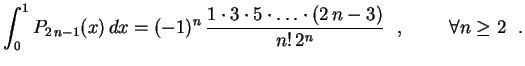
$\displaystyle \int_0^1P_{2\,n-1}(x)\,dx=(-1)^n\,\frac {1\cdot3\cdot5\cdot\ldots\cdot(2\,n-3)} {n!\,2^n} \ \ , \qquad\ \forall n\geq 2 \ \ . $

Usando este fato, obtém-se

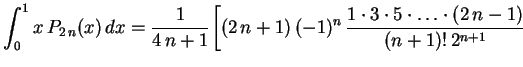
$\displaystyle \int_0^1x\,P_{2\,n}(x)\,dx=\frac{1}{4\,n+1}\biggl[ (2\,n+1)\,(-1)^n\,\frac{1\cdot3\cdot5\cdot\ldots\cdot (2\,n-1)}{(n+1)!\,2^{n+1}} \hspace{3.0cm} $


$\displaystyle \hspace{6.0cm} +2\,n\,(-1)^{n-1}\,\frac {1\cdot3\cdot5\cdot\ldots\cdot(2\,n-3)} {n!\,2^n}\biggr] \ \ , $

de onde segue

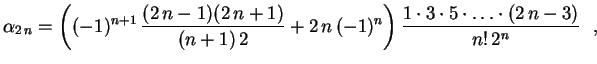
$\displaystyle \alpha_{2\,n}=\left((-1)^{n+1}\,\frac{(2\,n-1) (2\,n+1)}{(n+1)\,2... ...,n\,(-1)^n\right)\frac {1\cdot3\cdot5\cdot\ldots\cdot(2\,n-3)} {n!\,2^n} \ \ , $

ou seja,

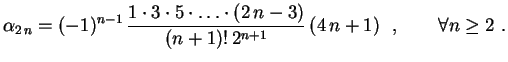
$\displaystyle \alpha_{2\,n}=(-1)^{n-1}\,\frac {1\cdot3\cdot5\cdot\ldots\cdot(2\,n-3)} {(n+1)!\,2^{n+1}}\,(4\,n+1) \ \ , \qquad \forall n\geq 2 \ . $

Calculamos separado,

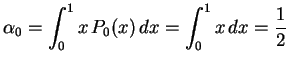
$\displaystyle \alpha_0=\int_0^1x\,P_0(x)\,dx=\int_0^1x\,dx=\frac{1}{2} $

e

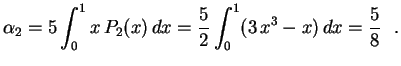
$\displaystyle \alpha_2=5\int_0^1x\,P_2(x)\,dx=\frac{5}{2} \int_0^1(3\,x^3-x)\,dx=\frac{5}{8} \ \ . $

Obtemos, assim, a expansão

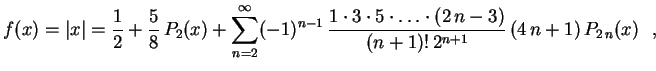
$\displaystyle f(x)=\lvert x\rvert=\frac{1}{2}+\frac{5}{8}\,P_2(x)+ \sum_{n=2}^\... ...\cdot5\cdot\ldots\cdot(2\,n-3)} {(n+1)!\,2^{n+1}}\,(4\,n+1)\,P_{2\,n}(x) \ \ , $

$ \forall x\in[-1,\,1] \ .$ Para ilustrar a representação acima, vejamos os gráficos de algumas das somas parciais da série construídos usando o maple.

Começamos carregando o pacote de polionômios ortogonais.


> with(orthopoly);

Definimos a soma parcial levando em conta que

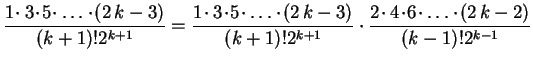
$\displaystyle \frac{1\!\cdot3\!\cdot\!5\!\cdot\ldots\cdot\!(2\,k-3)}{(k+1)!2^{k... ...1}}\cdot \frac{2\!\cdot4\!\cdot\!6\!\cdot\ldots\cdot\!(2\,k-2)}{(k-1)!2^{k-1}} $

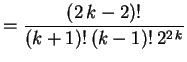
$\displaystyle =\frac{(2\,k-2)!}{(k+1)!\,(k-1)!\,2^{2\,k}} $

> S:=(n,x)->1/2+5/8*P(2,x)+
sum((-1)^(k-1)*(2*k-2)!/((k+1)!*2^(k+1)*(k-1)!*2^(k-1))*(4*k+1)*P(2*k,x),k=2..n);

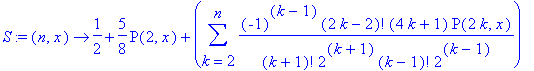
Abaixo construímos algumas somas parciais, mostrando seus gráficos junto com a própria função.

> S(2,x);

> S(3,x);

> plot([S(2,x),S(3,x),abs(x)], x=-1..1,color=[red,blue,black],scaling=CONSTRAINED);

[Maple Plot]

> S(5,x);

> evalf(S(5,x));


> sort(evalf(S(6,x)));


> plot([S(5,x),S(6,x),abs(x)],x=-1..1,color=[red,blue,black],scaling=CONSTRAINED);

[Maple Plot]



Aplicações



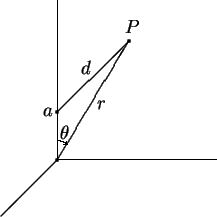
1. Potencial Gerado por uma Carga Pontual fora da Origem

Vamos dar uma aplicação concreta da função geradora dos polinômios de Legendre. Consideremos uma carga $ q$ no ponto $ \,(0,0,a)\,$.


   \begin{picture}(170,150) \par\put(40,50){\line(1,0){100}} \par\put(40,50){\line(... ... \par\put(46,59.7){\line(0,1){2}} \par\put(42,63){\mbox{$\theta$}} \end{picture}      

$\displaystyle d^2=a^2+r^2-2\,a\,r\,\cos\theta \ . $

O potencial $ \,u\,$ no ponto $ P\,$, gerado pela carga $ \,q\,$, vale

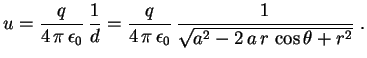
$\displaystyle u=\frac{q}{4\,\pi\,\epsilon_0}\,\frac{1}{d}= \frac{q}{4\,\pi\,\epsilon_0}\, \frac{1}{\sqrt{a^2-2\,a\,r\,\cos\theta+r^2}} \ . $

Na região $ \,r<a\,$, vale
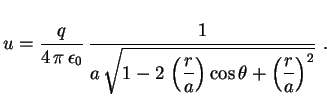
$\displaystyle u=\frac{q}{4\,\pi\,\epsilon_0}\,\frac{1}{a\,\displaystyle \sqrt{1-2\,\left(\frac{r}{a}\right)\cos\theta+ \left(\frac{r}{a}\right)^2}} \ . $

Usando a função geradora dos polinômios de Legendre temos

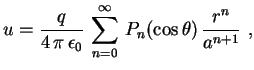$\displaystyle u=\frac{q}{4\,\pi\,\epsilon_0}\,\sum_{n=0}^\infty\, P_n(\cos\theta)\,\frac{r^n}{a^{n+1}} \ ,$    se$\displaystyle \quad r<a\,. $

Na região $ \,r>a\,$ vale

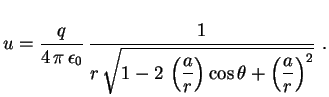
$\displaystyle u=\frac{q}{4\,\pi\,\epsilon_0}\,\frac{1}{r\,\displaystyle \sqrt{1-2\,\left(\frac{a}{r}\right)\cos\theta+ \left(\frac{a}{r}\right)^2}} \ . $
e, portanto,

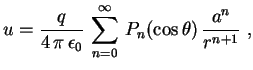$\displaystyle u=\frac{q}{4\,\pi\,\epsilon_0}\,\sum_{n=0}^\infty\, P_n(\cos\theta)\,\frac{a^n}{r^{n+1}} \ ,$    se$\displaystyle \quad r>a \ . $



2. Potencial do Dipolo

Suponhamos que temos cargas $ \,\pm q\,$ nos pontos $ \,(0,0,\pm a)\,$. Usando a fórmula acima, o potencial longe do dipolo será dado por

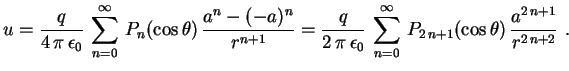
$\displaystyle u=\frac{q}{4\,\pi\,\epsilon_0}\,\sum_{n=0}^\infty\, P_n(\cos\thet... ...,\sum_{n=0}^\infty\, P_{2\,n+1}(\cos\theta)\,\frac{a^{2\,n+1}}{r^{2\,n+2}} \ . $

Bem afastado do dipolo, para $ \,r\gg a\,$, só o primeiro termo da série já dá uma boa aproximação

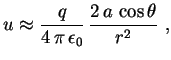
$\displaystyle u\approx\frac{q}{4\,\pi\,\epsilon_0}\,\frac{2\,a\,\cos\theta} {r^2} \ , $

ou,

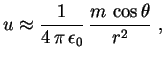
$\displaystyle u\approx\frac{1}{4\,\pi\,\epsilon_0}\,\frac{m\,\cos\theta} {r^2} \ , $

onde $ \,m=2\,a\,$ é chamado de momento do dipolo. Esta última aproximação é muito usada em Física.


Eduardo H. M. Brietzke