Vamos estudar a equação de Legendre
Para
Conclusão: Para
![]()
![]() é um parâmetro real a ser escolhido. Vamos ver
adiante que esta equação é
muito importante nas aplicações.
é um parâmetro real a ser escolhido. Vamos ver
adiante que esta equação é
muito importante nas aplicações. ![]() é um ponto ordinário, pois as funções
é um ponto ordinário, pois as funções
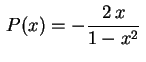 e
e
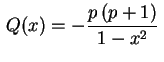 são analíticas neste ponto. Suas séries têm
raio de convergência
são analíticas neste ponto. Suas séries têm
raio de convergência ![]() (são séries geométricas
de razão
(são séries geométricas
de razão
![]() , por exemplo,
, por exemplo,
![]() ).
Logo a solução é da forma
).
Logo a solução é da forma
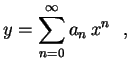
![]() . Substituindo na
equação temos
. Substituindo na
equação temos
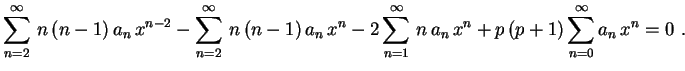
![]() no
1
no
1![]() somatório, ele se transforma em
somatório, ele se transforma em
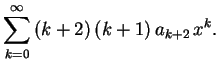
![]() ,
inclusive a letra
,
inclusive a letra ![]() novamente. O 2
novamente. O 2![]() e o terceiro somatórios podem ser começados em
e o terceiro somatórios podem ser começados em ![]() (fazendo isto entram mais duas parcelas para a soma, só
que são ambas nulas) . Feito isto, podemos reunir todos
os termos em um único somatório
(fazendo isto entram mais duas parcelas para a soma, só
que são ambas nulas) . Feito isto, podemos reunir todos
os termos em um único somatório
![$\displaystyle \sum_{n=0}^\infty\biggl[(n+2)\,(n+1)\,a_{n+2}-
\left((n\,(n+1)-p\,(p+1)\rule{0.0cm}{0.4cm}\right)a_n\biggr]x^n=0 \ \ .
$](img19.gif)
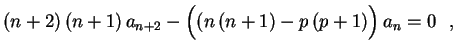 para
para ![]()
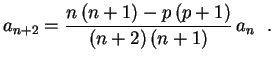
![]() como variável e
como variável e ![]() como constante, o trinômio
como constante, o trinômio
![]()
![]() e
e
![]() e, portanto, se fatora como
e, portanto, se fatora como
![]()
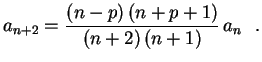
![]() e
e ![]() e depois
e depois
![]() e
e ![]() , obtemos
, obtemos
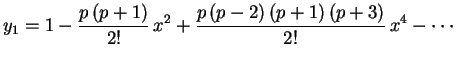
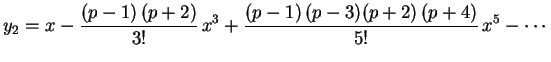 ,
,
![]() .
Uma observação extremamente importante é que se
.
Uma observação extremamente importante é que se
![]() , então uma destas duas
soluções é um polinômio de grau
, então uma destas duas
soluções é um polinômio de grau ![]() . Por exemplo,
. Por exemplo,
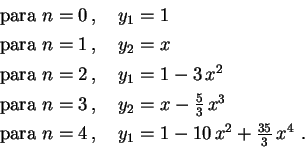
![]() . Normalizados desta maneira,
são chamados de polinômios de Legendre e denotados
por
. Normalizados desta maneira,
são chamados de polinômios de Legendre e denotados
por
![]() . Assim
. Assim
![]() e
e
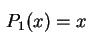 .
.
Para ![]() ,
,
![]() satisfaz
satisfaz
![]() .
Logo
.
Logo
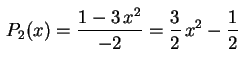 .
.
Para ![]() ,
,
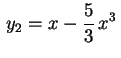 satisfaz
satisfaz
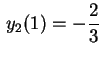 e,
portanto,
e,
portanto,
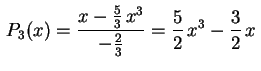 .
.
Analogamente se deduz que
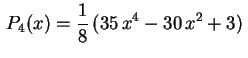 .
.
Para ver uma lista dos primeiros polinômios de Legendre e seus
gráficos, clique aqui
Vamos encontrar outra solução linearmente
independente para a equação de Legendre pelo método
visto na 1![]() área.
área.
![]() , procuramos outra solução na forma
, procuramos outra solução na forma
![]() .
É fácil ver que
.
É fácil ver que ![]() deve satisfazer
deve satisfazer
![]()
![]() ,
se reduz à equação separável de
1
,
se reduz à equação separável de
1![]() ordem
ordem
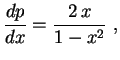
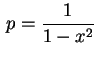 . Segue que
. Segue que
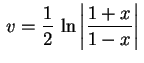 .
Como estamos interessados em resolver a equação
no intervalo
.
Como estamos interessados em resolver a equação
no intervalo
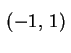 , podemos
dispensar os módulos e, finalmente,
, podemos
dispensar os módulos e, finalmente,
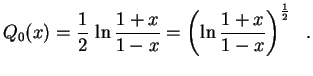
![]() e
e
![]()
![]() ,
concluímos então que, para
,
concluímos então que, para
![]() ,
, ![]() .
.
![]() , a equação
de Legendre tem duas soluções
linearmente independentes, uma delas o polinômio
, a equação
de Legendre tem duas soluções
linearmente independentes, uma delas o polinômio
![]() e a outra a função
e a outra a função
![]() ilimitada
no intervalo
ilimitada
no intervalo
![]() . Logo as únicas soluções limitadas
no intervalo
. Logo as únicas soluções limitadas
no intervalo
![]() são os múltiplos
de
são os múltiplos
de
![]() .
.
Para ![]() , de maneira análoga,
duas soluções linearmente independentes são
, de maneira análoga,
duas soluções linearmente independentes são
![]() e
e 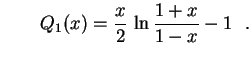
![]()
![]() as únicas soluções limitadas no intervalo
as únicas soluções limitadas no intervalo
![]() são os múltiplos de
são os múltiplos de
![]() .
.
Continuando este mesmo procedimento, para ![]() ,
temos
,
temos
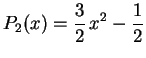 e
e 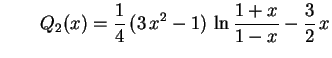
![]() ,
,
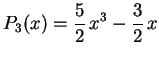 e
e 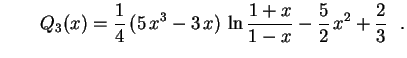
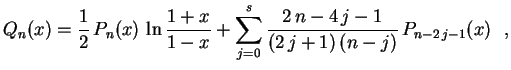
![$ \displaystyle s=\biggl[\frac{n-1}{2}\biggr]$](img80.gif) é o maior
inteiro que é menor ou igual a
é o maior
inteiro que é menor ou igual a
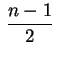 .
.
Conclusão: Qualquer que seja
![]() , as únicas soluções
limitadas no intervalo
, as únicas soluções
limitadas no intervalo
![]() da equação
de Legendre são os múltiplos do polinômio
da equação
de Legendre são os múltiplos do polinômio
![]() .
.
OBS. Um fato verdadeiro, mas que
não ficou justificado ainda, é que para outros
valores de ![]() , que não os da forma
, que não os da forma
![]() , a equação de Legendre não
tem solução limitada no intervalo
, a equação de Legendre não
tem solução limitada no intervalo
![]() ,
além da trivial. Os livros que dão um tratamento
mais elementar costumam ser omissos neste ponto, mas
vamos dar aqui uma justificativa, (conforme
Courant-Hilbert, Methods of Mathematical Physics,
vol. 1, pag. 325).
,
além da trivial. Os livros que dão um tratamento
mais elementar costumam ser omissos neste ponto, mas
vamos dar aqui uma justificativa, (conforme
Courant-Hilbert, Methods of Mathematical Physics,
vol. 1, pag. 325).
Afirmação: Se ![]() não é
um inteiro
não é
um inteiro ![]() , não existe solução que
seja limitada no intervalo
, não existe solução que
seja limitada no intervalo
![]() para
a equação de Legendre
para
a equação de Legendre
![]()
![]() .
.
Demonstração:
Começamos notando que se ![]() é uma solução da equação de Legendre,
então
é uma solução da equação de Legendre,
então ![]() também é. Logo as funções
também é. Logo as funções
![]() e
e
![]() também são soluções. Mas
também são soluções. Mas
![]() é par e
é par e
![]() é ímpar, com
é ímpar, com
![]() . Portanto, para provar
que se
. Portanto, para provar
que se ![]() não é um inteiro
não é um inteiro ![]() a
equação de Legendre não tem solução
não trivial limitada no intervalo
a
equação de Legendre não tem solução
não trivial limitada no intervalo
![]() ,
basta provar que não existe uma solução
limitada que seja par ou ímpar.
Basta mostrar que se
,
basta provar que não existe uma solução
limitada que seja par ou ímpar.
Basta mostrar que se ![]() for uma solução da equação de Legendre,
limitada no intervalo
for uma solução da equação de Legendre,
limitada no intervalo
![]() , par ou
ímpar, então
, par ou
ímpar, então ![]() para algum
para algum
![]() e
e ![]() é um polinômio.
Chamamos
é um polinômio.
Chamamos
![]() .
A fórmula de recorrência pode ser reescrita como
.
A fórmula de recorrência pode ser reescrita como
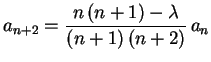
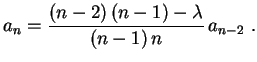
![]() par (ímpar) vamos ter
par (ímpar) vamos ter ![]() somente para
somente para ![]() par (ímpar). Vamos supor que
uma dessas duas situações ocorre.
Aplicando a recorrência repetidas vezes obtemos
par (ímpar). Vamos supor que
uma dessas duas situações ocorre.
Aplicando a recorrência repetidas vezes obtemos
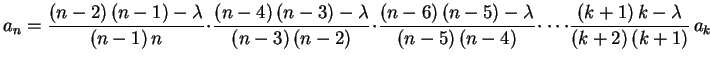
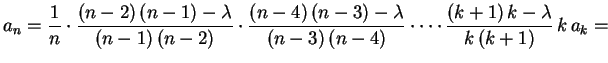
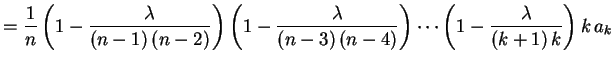
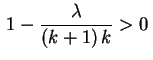 .
Para concluir o raciocínio, necessitamos um
resultado auxiliar.
.
Para concluir o raciocínio, necessitamos um
resultado auxiliar.
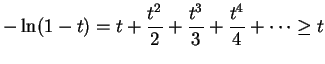
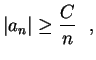 para todo
para todo 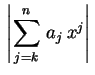 se torna arbitrariamente grande para
se torna arbitrariamente grande para 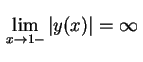 ,
provando a afirmação.
,
provando a afirmação.
![$\displaystyle P_n(x)=\frac{1}{n!\,2^n}\,\frac{d^n}{dx^n}\,
\biggl[\left(x^2-1\rule{0.0cm}{0.4cm}\right)^n\biggr] \ \ .
$](img127.gif)
![$ \displaystyle\,R_n(x)=\frac{1}{n!\,2^n}\,
\frac{d^n}{dx^n}\,\biggl[\left(x^2-1\rule{0.0cm}{0.4cm}
\right)^n\biggr]\,\rule{0.0cm}{0.7cm}$](img128.gif) .
.
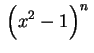 tem grau
tem grau 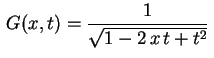 satisfaz
satisfaz
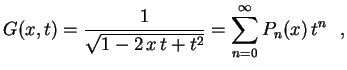 para
para 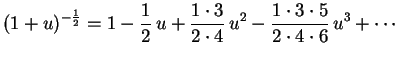
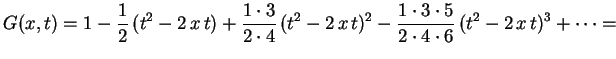
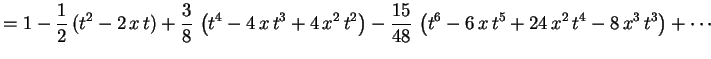
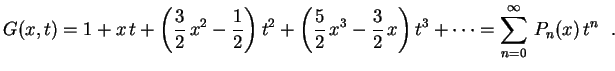
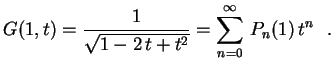
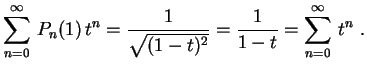
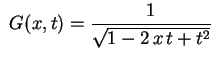 satisfaz
satisfaz
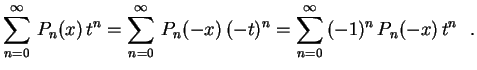
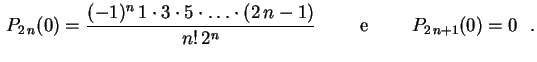
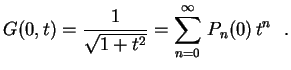
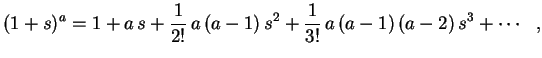
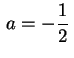 , obtemos
, obtemos
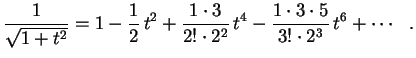
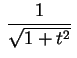 , obtemos
, obtemos
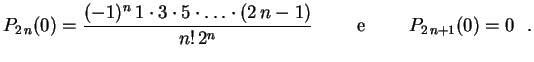
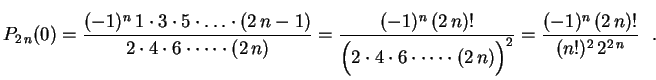
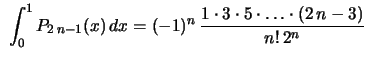 , para
, para 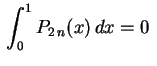 ,
para
,
para
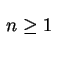 .
.
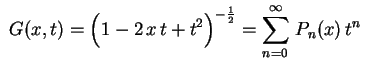 em relação a
em relação a 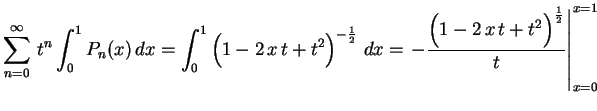
![$\displaystyle =\biggl[\left(1+t^2\right)^\frac{1}{2}-(1-t)\biggr]=
\frac{1}{t}\...
...2!}\,\frac{1}{2^2}\,t^4+
\frac{1}{3!}\,\frac{1\cdot 3}{2^3}\,t^6-\cdots\biggr]
$](img172.gif)
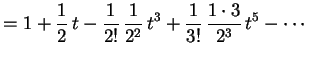
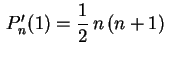 .
.
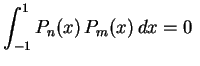 , para
, para
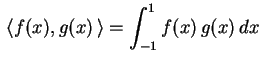 .
.
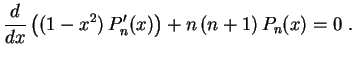
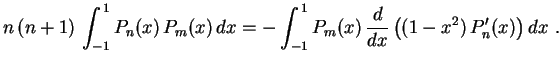
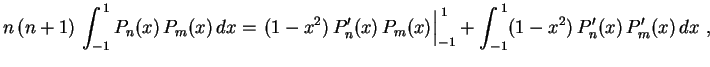
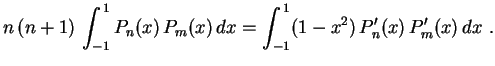
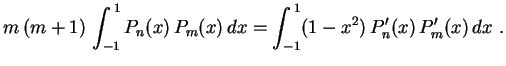
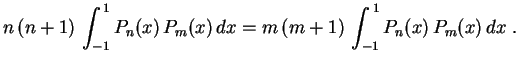
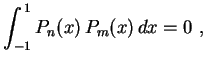 se
se 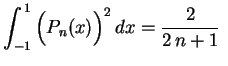
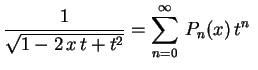 por si própria, obtemos
por si própria, obtemos
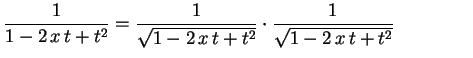
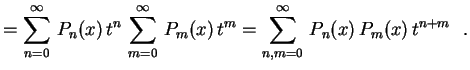
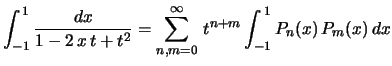
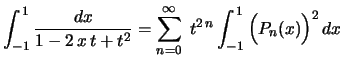
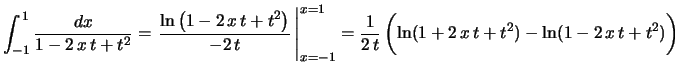
![$\displaystyle =\frac{1}{t}\left(\ln(1+t)-\ln(1-t)\rule{0.cm}{0.4cm}\right)
=\fr...
...right)+\left(t+\frac{t^2}{2}+
\frac{t^3}{3}+\frac{t^4}{4}+\cdots\right)\biggr]
$](img199.gif)
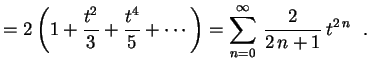
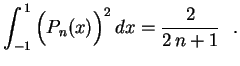
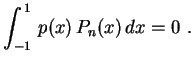
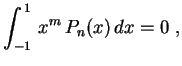 para todo
para todo