Seja 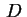 o disco
o disco
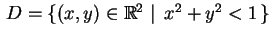 e denotemos por
e denotemos por
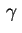 a sua
circunferência. Vamos determinar os autovalores e as
autofunções do laplaciano no disco
a sua
circunferência. Vamos determinar os autovalores e as
autofunções do laplaciano no disco 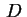 , isto é,
vamos considaderar o problema
, isto é,
vamos considaderar o problema
![$\displaystyle \left\{
\begin{array}{l}
\Delta\,\phi\,=\phi_{rr}+\displaystyle
\...
...a )=0 \rule[0.6cm]{0cm}{0cm} \ \ , \ \ \text{ em } \ \gamma
\end{array}
\right.$](img4.gif) |
(1) |
Pelo método de separação de variáveis,
procuramos a autofunção na forma
Substituindo em (1) temos
Temos, então,
![$\displaystyle \left\{
\begin{array}{l}
\psi''(\theta )+\mu \,\,\psi(\theta )=0 \\
\psi (\theta+2\,\pi)=\psi(\theta) \rule[0.6cm]{0cm}{0cm}
\end{array}
\right.$](img8.gif) |
(2) |
e
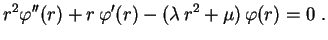 |
(3) |
Como já vimos antes, as soluções não triviais
de (2) são:
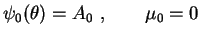 |
(4) |
e
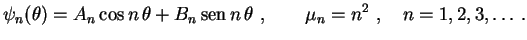 |
(5) |
Pondo estes valores de 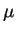 na equação (3) e pondo também
na equação (3) e pondo também
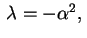 com
com
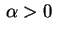 ,
pois sabemos que para qualquer região
,
pois sabemos que para qualquer região 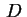 os
autovalores do laplaciano são todos negativos, temos
os
autovalores do laplaciano são todos negativos, temos
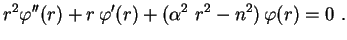 |
(6) |
A equação (6) se reduz a uma equação de Bessel
através da mudança de variável
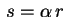 .
De fato, pela regra da cadeia,
.
De fato, pela regra da cadeia,
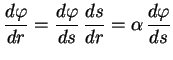 |
(7) |
e, multiplicando por 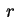 ,
,
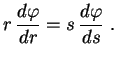 |
(8) |
Derivando (7) mais uma vez e usando novamente a regra da cadeia, obtemos
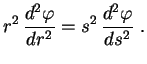 |
(9) |
Substituindo (8) e (9) na equação (6), obtemos
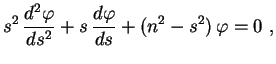 |
(10) |
que é a equação de Bessel de índice 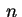 .
Portanto, se pensarmos em
.
Portanto, se pensarmos em
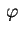 expressa como
função de
expressa como
função de 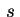 e não de
e não de 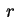 , teremos
, teremos
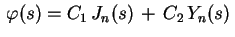 .
Voltando a expressar
.
Voltando a expressar
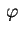 em função de
em função de 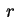 ,
,
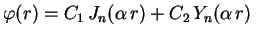 .
Lembrando agora que as funções envolvidas devem ser
finitas e estar bem definidas para
.
Lembrando agora que as funções envolvidas devem ser
finitas e estar bem definidas para 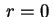 , pois
, pois 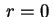 corresponde à origem, que é um ponto do disco
corresponde à origem, que é um ponto do disco  ,
vê-se que é preciso que
,
vê-se que é preciso que 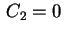 , ou seja,
Nossa conclusão, até agora, é que as funções
, ou seja,
Nossa conclusão, até agora, é que as funções
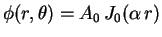 |
(11) |
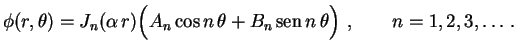 |
(12) |
satisfaz
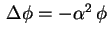 . Precisamos ainda verificar
para quais valores de
. Precisamos ainda verificar
para quais valores de
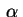 a função
a função 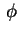 cumpre também a condição de fronteira
cumpre também a condição de fronteira
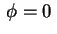 em
em
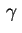 , isto é,
, isto é,
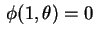 . Tanto para (11)
quanto para (12), de
. Tanto para (11)
quanto para (12), de
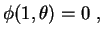
para todo
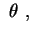
segue que
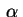 deve cumprir a condição
deve cumprir a condição
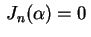 , isto é,
, isto é,
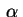 deve ser um dos
zeros (positivos) da função de Bessel
deve ser um dos
zeros (positivos) da função de Bessel 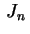 .
Sabemos que
.
Sabemos que 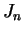 se anula para uma infinidade de zeros.
Existe toda uma seqüência de zeros positivos de
se anula para uma infinidade de zeros.
Existe toda uma seqüência de zeros positivos de 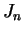 Conclusão: Os autovalores do laplaciano no disco
Conclusão: Os autovalores do laplaciano no disco 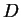 são
são
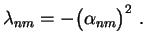 |
(13) |
A uma autovalor da forma
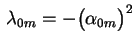 corresponde a autofunção
corresponde a autofunção
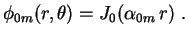 |
(14) |
A um autovalor
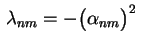 com
com
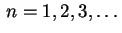 correspondem duas autofunções linearmente
independentes
correspondem duas autofunções linearmente
independentes
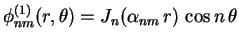 e e 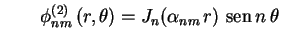 |
(15) |
As autofunções (14) são funções radiais, isto é, dependem
somente da coordenada polar 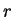 , ou seja, suas curvas de nível são
os círculos centrados na origem, ou ainda, seus gráficos são
superfícies de revolução.
Qualquer combinação linear de
, ou seja, suas curvas de nível são
os círculos centrados na origem, ou ainda, seus gráficos são
superfícies de revolução.
Qualquer combinação linear de
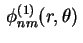 e
e
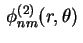 dadas por (15)
é autofunção correspondente ao autovalor
dadas por (15)
é autofunção correspondente ao autovalor
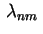 ,
,
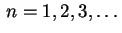 . Logo qualquer função da forma
. Logo qualquer função da forma
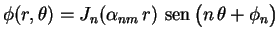 |
(16) |
é uma autofunção correspondente ao autovalor
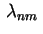 .
Todas as autofunções (16) são obtidas de
.
Todas as autofunções (16) são obtidas de
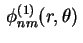 por uma rotação.
por uma rotação.
Ortogonalidade. Vimos na parte 1
que as autofunções do laplaciano em
um domínio 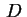 qualquer são ortogonais. Lembrando que
qualquer são ortogonais. Lembrando que
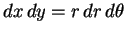 , vemos que neste caso a ortogonalidade se
traduz por
, vemos que neste caso a ortogonalidade se
traduz por
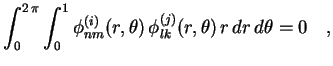 se se 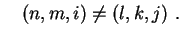 |
(17) |
Na verdade, para muitos valores dos índices, esta informação
poderia ter sido facilmente obtida diretamente. Por exemplo,
pela ortogonalidade do sistema de senos e cossenos
em
![$ \,[0, 2\,\pi]\,$](img61.gif) . No entanto, a relação de ortogonalidade
(17) nos dá uma conclusão não trivial no caso
. No entanto, a relação de ortogonalidade
(17) nos dá uma conclusão não trivial no caso 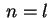 ,
,
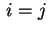 , que é
, que é
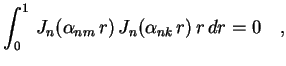 se se 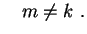 |
(18) |
Em outras palavras, para qualquer 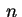 , as funções
, as funções
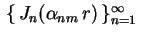 constituem um sistema ortogonal em relação ao
produto interno
constituem um sistema ortogonal em relação ao
produto interno
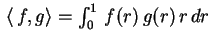 ,
ou ainda, na nomenclatura mais clássica, são ortogonais
no intervalo
,
ou ainda, na nomenclatura mais clássica, são ortogonais
no intervalo ![$ \,[0,1]\,$](img68.gif) em relação ao peso
em relação ao peso
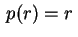 . Note a semelhança com a ortogonalidade,
por exemplo dos
. Note a semelhança com a ortogonalidade,
por exemplo dos
 no intervalo
no intervalo
![$ \,[0,1]\,$](img68.gif) . Os
. Os  são justamente os zeros
positivos da função
são justamente os zeros
positivos da função
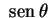 . Assim também
os
. Assim também
os
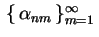 são os
zeros positivos da função
são os
zeros positivos da função
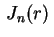 . Do mesmo modo
que os
. Do mesmo modo
que os
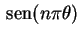 são ortogonais em
são ortogonais em ![$ \,[0,1]\,$](img68.gif) ,
os
,
os
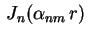 também são, devendo-se
ter o cuidado de escolher o peso conveniente. Devemos
mencionar, ainda, que a relação de ortogonalidade (17)
das funções de Bessel pode ser deduzida
fora do contexto das autofunções
do laplaciano no disco, usando somente propriedades das
funções de Bessel. Isto pode ser visto na maioria
dos livros que tratam de funções de Bessel, por exemplo,
também são, devendo-se
ter o cuidado de escolher o peso conveniente. Devemos
mencionar, ainda, que a relação de ortogonalidade (17)
das funções de Bessel pode ser deduzida
fora do contexto das autofunções
do laplaciano no disco, usando somente propriedades das
funções de Bessel. Isto pode ser visto na maioria
dos livros que tratam de funções de Bessel, por exemplo,
Bowman, F. - Introduction to Bessel Functions (página 108,
fórmula (6.62) )
Esta relação de ortogonalidade abre a
possibilidade para o seguinte tipo de expansão:
Dada uma função
![$ \,f:[0,1]\longrightarrow\mathbb{R}\,$](img77.gif) e fixado um
e fixado um 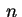 , expressar
, expressar 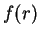 como
como
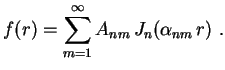 |
(19) |
Resulta que a expansão acima, chamada de série de
Fourier-Bessel, é possível para toda função
razoável. Para calcular os coeficientes 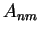 precisamos
ainda da expressão das normas:
precisamos
ainda da expressão das normas:
Prop.
![$ \displaystyle\left\Vert \,J_n\right\Vert^2
=\left\langle \,J_n\,,\,J_n\,\right...
...pha_{nm})\right]^2=
\frac{1}{2}\left[ J_n^{\,\prime }(\alpha_{nm})\right]^2 \ .$](img81.gif)
Não vamos aqui dar a demonstração deste
fato, que também pode ser vista no livro de Bowman citado
acima (fórmula (6.63) ). Vamos apenas assinalar que dela decorre,
como nas séries de Fourier, que, na expansão (19), os
coeficientes são dados por
![$\displaystyle A_{nm}=\frac{2}{\left[ J_{n+1}(\alpha_{nm})\right]^2}\,
\int_0^1\,f(r)\,J_n(\alpha_{nm}\,r)\,r\,dr \ .$](img82.gif) |
(20) |
Exemplo. Expandir a função constante
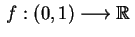 ,
,
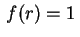 em série de Fourier-Bessel
De acordo com (20), os coeficientes são dados por
Conforme vimos em um dos exercícios sobre funções de
Bessel, a partir das expressões em séries de potências para
em série de Fourier-Bessel
De acordo com (20), os coeficientes são dados por
Conforme vimos em um dos exercícios sobre funções de
Bessel, a partir das expressões em séries de potências para
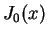 e para
e para 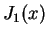 , pode-se facilmente verificar que
Segue que
Logo
e, finalmente,
, pode-se facilmente verificar que
Segue que
Logo
e, finalmente,
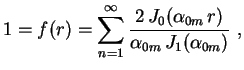
para
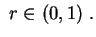
Para ver os gráficos de algumas somas parciais desta expansão
clique aqui.
Pode-se expandir a mesma função usando 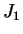 em lugar de
em lugar de 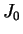 .
.
Aplicação à membrana vibrante circular.
As ondas estacionárias na membrana circular são, por (16), da forma
onde
ou, equivalentemente,
A primeira das expressões acima para 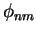 permite facilmente
identificar as linhas nodais desta onda estacionária:
permite facilmente
identificar as linhas nodais desta onda estacionária:
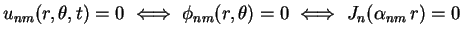
ou
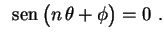
(O símbolo ``
 " significa ``se e somente se").
Como
" significa ``se e somente se").
Como 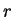 varia no intervalo
varia no intervalo ![$ [0,1]$](img110.gif) ,
,
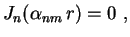
para
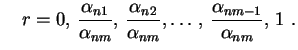
Segue daí que os círculos centrados da origem com raios da forma
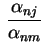 ,
,
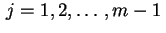 são linhas nodais.
Além disto,
sobre
são linhas nodais.
Além disto,
sobre 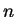 diâmetros do disco unitário
diâmetros do disco unitário 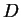 (estes diâmetros dividem
(estes diâmetros dividem
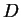 em partes iguais). Estes diâmetros também
são, portanto, linhas nodais.
em partes iguais). Estes diâmetros também
são, portanto, linhas nodais.
Caso particular - vibrações com simetria radial. Este
é o caso particular em que a função
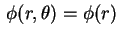 depende só de
depende só de 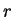 . Por (14), as ondas estacionárias com simetria
radial são da forma
As linhas nodais são os círculos
. Por (14), as ondas estacionárias com simetria
radial são da forma
As linhas nodais são os círculos
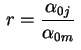 ,
,
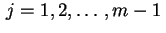 .
.
Para ver os gráficos de algumas autofunções
do laplaciano no disco, bem como animações das
correspondentes ondas estacionárias na membrana circular,
clique aqui
![$\displaystyle \left\{
\begin{array}{l}
\Delta\,\phi\,=\phi_{rr}+\displaystyle
\...
...a )=0 \rule[0.6cm]{0cm}{0cm} \ \ , \ \ \text{ em } \ \gamma
\end{array}
\right.$](img4.gif)
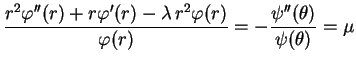
![$\displaystyle \left\{
\begin{array}{l}
\psi''(\theta )+\mu \,\,\psi(\theta )=0 \\
\psi (\theta+2\,\pi)=\psi(\theta) \rule[0.6cm]{0cm}{0cm}
\end{array}
\right.$](img8.gif)
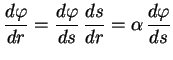
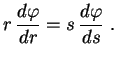
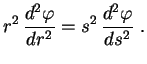
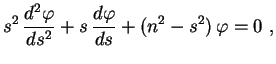
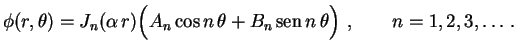
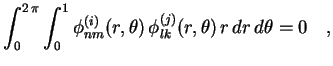 se
se 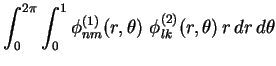
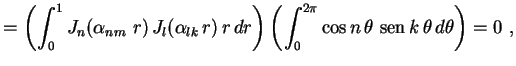
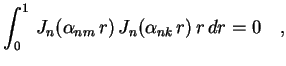 se
se 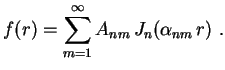
![$ \displaystyle\left\Vert \,J_n\right\Vert^2
=\left\langle \,J_n\,,\,J_n\,\right...
...pha_{nm})\right]^2=
\frac{1}{2}\left[ J_n^{\,\prime }(\alpha_{nm})\right]^2 \ .$](img81.gif)
![$\displaystyle A_{nm}=\frac{2}{\left[ J_{n+1}(\alpha_{nm})\right]^2}\,
\int_0^1\,f(r)\,J_n(\alpha_{nm}\,r)\,r\,dr \ .$](img82.gif)
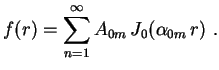
![$\displaystyle A_{0m}=\frac{2}{\left[ J_1(\alpha_{0m})\right]^2}\,
\int_0^1J_0(\alpha_{0m}\,r)\,r\,dr \ .
$](img86.gif)
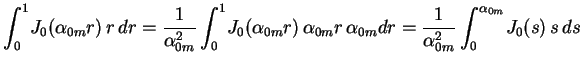
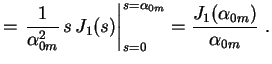
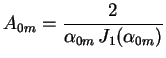
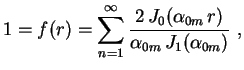 para
para ![]() em lugar de
em lugar de ![]() .
.
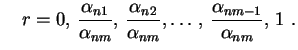
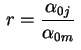 ,
,