© 2001-2019 Instituto de Matemática e Estatística — UFRGS

MAT 01354   Cálculo e Geometria Analítica IIA

QUÁDRICAS:
O Hiperbolóide Elíptico de Uma Folha

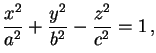
Hiperbolóide Elíptico de Uma Folha A equação-padrão do hiperbolóide elíptico de uma folha é

Equação-Padrão do Hiperbolóide Elíptico de Uma Folha

sendo convencionado que os parâmetros a, b e c são todos positivos. Os parâmetros a e b são os semi-eixos da elipse obtida no corte deste hiperbolóide pelo plano coordenado z = 0, dada pela equação

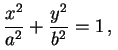
Equação do Corte do Hiperbolóide Elíptico de Uma Folha com o Plano xy
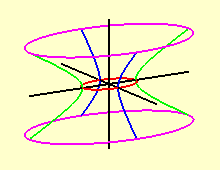
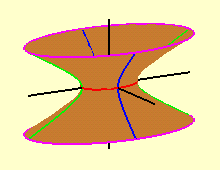que está no "gargalo" do hiperbolóide elíptico de uma folha; nas figuras abaixo, esta elipse aparece em vermelho. Os Cortes do Hiperbolóide Elíptico de Uma Folha pelos Planos Coordenados Os Cortes do Hiperbolóide Elíptico de Uma Folha pelos Planos Coordenados Os cortes do hiperbolóide elíptico de uma folha com os planos coordenados verticais são as hipérboles que aparecem nas cores verde e azul nas figuras ao lado; à esquerda temos as duas hipérboles no hiperbolóide elíptico de uma folha transparente e à direita aparecem (partes d)estas curvas no mesmo hiperbolóide elíptico de uma folha, agora pintado de marrom. Estas hipérboles, de equações Os Cortes do Hiperbolóide Elíptico de Uma Folha no Primeiro Octante
Equação do Corte do Hiperbolóide Elíptico de Uma Folha com os Planos xz e yz
são obtidas tomando y = 0 e x = 0 na equação-padrão. Nestas figuras também aparecem em carmim os cortes do hiperbolóide elíptico de uma folha por dois planos horizontais z = ± k, que são as elipses de equações
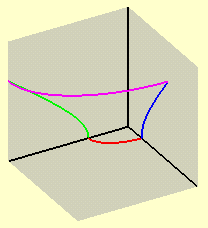
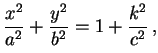
Equação do Corte do Hiperbolóide Elíptico de Uma Folha com Planos Horizontais
para qualquer constante k. Na figura à direita, vemos as partes de todas estas curvas que aparecem no primeiro octante.

         Convém observar que o que é exibido nestas figuras é só uma parte do hiperbolóide elíptico de uma folha, que se estende indefinidamente em todos os seis sentidos do espaço tridimensional; como ocorre com a hipérbole, no entanto, basta entender o comportamento do hiperbolóide na vizinhança da origem, pois o resto é bastante previsível. Também observamos que tomando a = b na equação-padrão, obtemos um hiperbolóide circular de uma folha , que sempre é uma superfície de revolução.

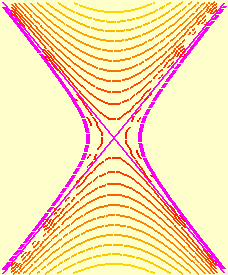
Curvas dos Cortes por Planos Verticais Paralelos aos Planos Coordenados

         Os cortes do hiperbolóide elíptico de uma folha com qualquer plano vertical paralelo a um dos planos coordenados x z ou y z sempre produz uma hipérbole, de equação

As Equações dos Cortes Verticais do Hiperbolóide Elíptico de Uma Folha
ou
As Equações dos Cortes Verticais do Hiperbolóide Elíptico de Uma Folha
tomando, respectivamente, y = ± k ou x = ± k constante. Na figura, a hipérbole limite em carmim é obtida pelos planos coordenados verticais pela origem; note que também há um outro corte carmim, que é o par de retas concorrentes que ocorre quando o plano vertical corta o "gargalo" do hiperbolóide.

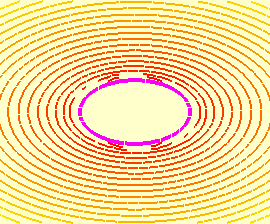
Curvas de Nível do Hiperbolóide Elíptico de Uma Folha

         O hiperbolóide elíptico de uma folha nunca é o gráfico de uma função real de duas variáveis reais pois quase sempre ocorrem dois cortes por retas verticais. No entanto, podemos separá-lo em dois gráficos, dados pelas duas funções

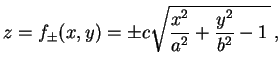
As Duas Funções Cujos Gráficos Formam o Hiperbolóide Elíptico de Uma Folha
cujo domínio é o anel plano ilimitado exterior ao "gargalo" do hiperbolóide. As curvas de nível de cada uma destas funções aparecem na figura: são as elipses vistas acima, dadas pelos cortes por planos horizontais, sendo que o "gargalo" sempre é a elipse mínima, que aparece em carmim.

         Concluímos esta visualização do hiperbolóide elíptico de uma folha deixando-o girar livremente em torno da origem:

O Hiperbolóide Elíptico de Uma Folha Girando em Torno da Origem


cone elíptico quádricas parabolóide elíptico