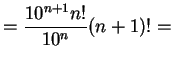
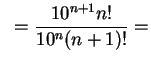
menos a mais pi terços e não de menos a menos pi terços*
no Volume 1
| de volta à página inicial do Cálculo IIA |
Errata da Reimpressão 2002 do
Anton:
Cálculo, um novo horizonte, Volume 2
| Pág. | linha | onde está | deveria ser |
| 51 | 2 | 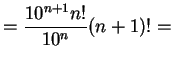 |
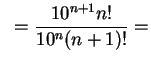 |
| 72 | 19 | f ' (0) x2 + | f ' (0) x + |
| 82 | 2 | k + 1k + 1 | (k + 1)k + 1 |
| 96 | 7 | (k + 2)2 | (k + 1)2 |
| 100 | – 11 | expandidia? | expandida? |
| 119 | Ex 29 | 1 – 1/22 + 1/32 + 1/42 + . . . | 1 – 1/22 + 1/32 – 1/42 + . . . |
| 123 | – 16 | 3m (1), | em (1), |
| 125 | Figura 3.1.9 | *O segundo Pi é 2 Pi* | |
| 125 | – 5 | 3.11.1 para | 3.1.1 para |
| 144 | 5 | (1 – cos q )2 dq = | (1/2) (1 – cos q )2 dq = |
| 145 | 7 | o cardióide | a cardióide |
| 145 | 17 | 12.3.6d e 12.3.6e: | 3.3.6d e 3.3.6e: |
| 145 | 18 e 19 | *o intervalo de integração das
quatro integrais simples é de menos a mais pi terços e não de menos a menos pi terços* | |
| 197 | Ex 27 | v = <0,1> | v = <2,1> |
| 215 | Ex 5 | <0, 1, 2>, | <0, 1, – 2>, |
| 225 | – 19 | v = <8, 5, 1> é | v = <8, 5, – 1> é |
| 231 | – 3 | ao plano x y têm | ao plano x z têm |
| 233 | CONE | nos planos y z e x y são | nos planos y z e x z são |
| 236 | – 13 | Na Seção 12.4, vimos | Na Seção 3.4, vimos |
| 238 | 6, 12 e 15 | z = – (x2 – y2) | z = – (x2 + y2) |
| 262 | – 7 | + t [ – sen t0) i + | + t [( – sen t0) i + |
| 262 | – 4 | x = cos t0 – sen t0 , | x = cos t0 – t sen t0 , |
| 317 | 3 | interceptos x ... interceptos y ... | interceptos x iguais a ... interceptos y iguais a ... |
| 344 | 17 | f x = 3 x3 y4 e | f x = 3 x2 y4 e |
| 345 | – 21 | (2 x sen y) | (2 y sen y) |
| 345 | – 17 | = 2 ex y cos y | = 2 y ex y cos y |
| 356 | 6 | e f x (x, y) = | e f y (x, y) = |
| 370 | – 7 | + 16(y – 1) + | + 16(y – 2) + |
| 372 | 17 | Delta z / z | | | Delta z / z | |
| 375 | 4 | se dz / dz e | se dz / dx e |
| 375 | Ex 2 | 4 z 3 ; | 4 z) 3 ; |
| 375 | Ex 3 | x = ln t , | x = 1 / t , |
| 376 | Ex 27 | P(3, 5, 1) | P(4, 6, 1) |
| 380 | Fig. 6.8.4 | * O parabolóide hiperbólico está impresso duplicado * | |
| 390 | – 1 | de restrição. Como o | de restrição. |
| 394 | 9 | que (2, 2, 4) é o ponto | que (2, 4, 4) é o ponto |
| 403 | 13 | (1 + 8xy) dxdy = | (1 + 8xy) dydx = |
| 405 | 4 | b, 0 | b, c |
| 418 | – 3 | [(1 + cos q )2 sen q | 2 [(1 + cos q )2 sen q |
| 446 | 8 | = 1/área de R = *integral dupla* | = 1/área de R *integral dupla* |
| 449 | 6 | é 2 p b 2, | é p b 2, |
| 455 | 3 | 13.8.2c , | 4.8.2c , |
| 496 | – 1 | x = t , x = t 2 | x = t , y = t 2 |
| 501 | 4 | (y i + j) | (y i + x j) |
| A14 | 3.1.5 | (d) ... (d) ... (d) | (d) ... (e) ... (f) |
| A16 | 3.3.3 | (a) ... (b) ... (b) | (a) ... (b) ... (c) |
| A21 | 4.6.9 | y + x = 1 | y + z = 1 |
| A24 | 4.8.31(b), 4.8.33(b) e 4.8.35(b) | r = | r = |
| A32 | 6.7.27 | 363 | *raiz de* 363 |
| A35 | 7.3.31 | (4/3) a3 | p a2 h |
| I-2 | Erro(s) | estimativas, 559-562 | estimativas, 559-562 no Volume 1 |
| de volta à página inicial do Cálculo IIA |
Elaborado durante 2001/2.
Atualização final em julho de 2002. |