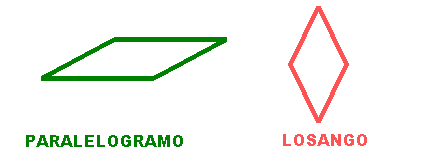
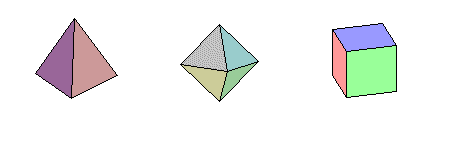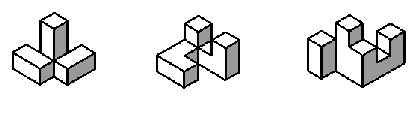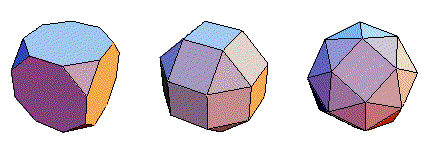ATIVIDADE II: Paralelogramo - Losango
ATIVIDADE III: Construindo Macros
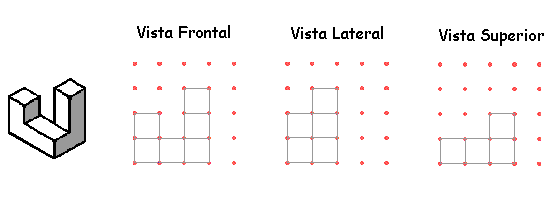
ATIVIDADE IV: Exercitando a Visão Espacial
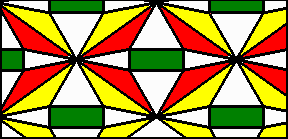
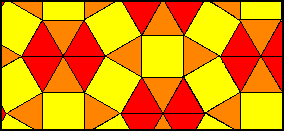
ATIVIDADE V: Mosaicos
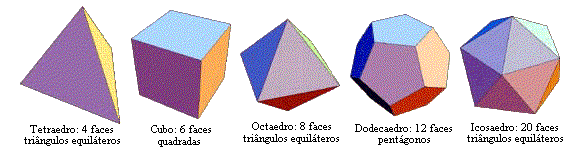
PROJETO: Poliedros Platônicos e Arquimedianos
ATIVIDADE I: Primeiras formas geométricas.
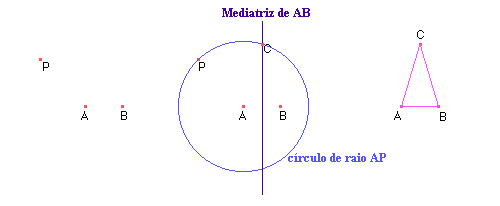
1. Triângulo Equilátero: é um polígono com três lados iguais.Vamos à construção! Lembre-se que o triângulo construído deve ser estável, ou seja, ao movimentarmos seus vértices, o triângulo continuará sendo equilátero.
- Construa um segmento de reta (Menu 3/Item 2)e chame
seus pontos extremos de A e B (Menu 10/Item 1).

- Construa uma circunferência com centro no ponto A e raio AB
(Menu 4/Item 1).
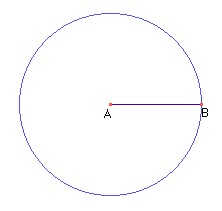
- Sobre a circunferência construída, marque um ponto (Menu 2/Item 2)
e chame-o de P (Menu 10/Item 1).
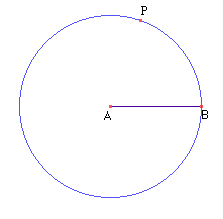
- Construa um segmento com extremos nos pontos A e P (Menu 3/Item 2).
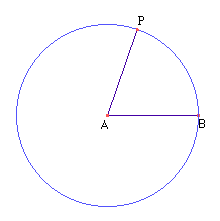
Meça os segmentos AB e AP (Menu 9/Item 1).
O que você descobriu?
Movimente o ponto P e tente descobrir qual a posição que ele
deve estar para que quando ligarmos os B e P o triângulo
ABP seja equilátero. - Construa agora uma circunferência com centro no ponto B e raio BA (Menu 4/Item 1). Sobre ela, marque um ponto
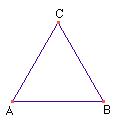
Experimente movimentar os pontos A e B e veja o que acontece. O triângulo ABC muda de tamanho, muda de posição mas permanece equilátero.
Observe que o ponto C não pode ser movido. Por que?
2. Triângulo Isósceles: é um triângulo dois lados iguais.
Vamos à construção! Lembre-se que o triângulo deve ser estável sob a ação do movimento.
- Construa um segmento de reta (Menu 3/Item 2) e chame seus
pontos extremos de A e B (Menu 10/Item 1).

- Marque o ponto médio desse segmento (Menu 5/Item 3) e chame-o de M (Menu 10/Item 1).
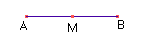
- Trace a reta perpendicular ao segmento AB que passa pelo ponto M (Menu 5/Item 1).
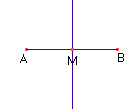
- Marque um ponto sobre a reta perpendicular que você construiu (Menu 2/Item 2) e chame-o
de C (Menu 10/Item 1).
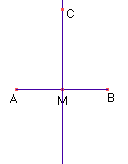
- Trace os segmentos AC e BC (Menu 3/Item 2). Você acabou de construir um triângulo
isósceles. Pode "esconder" a reta perpendicular e o ponto M (Menu 11/Item 1).
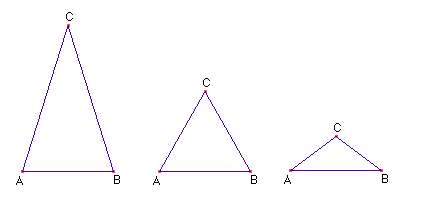
Movimente os pontos A, B e C e veja o que acontece. Mudamos o tamanho e a forma do triângulo mas ele continua sendo isósceles.
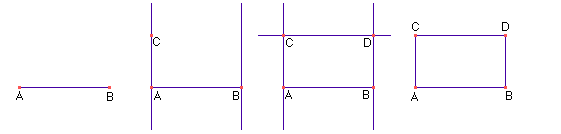
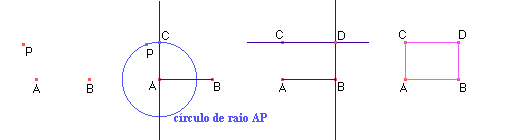
3. Quadrado: é um polígono com quatro lados e quatro ângulos retos.Siga os passos indicados no desenho para construir seu quadrado.
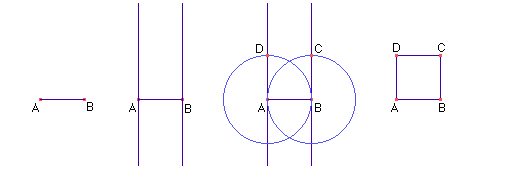
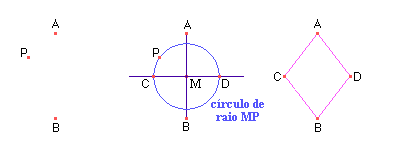
DESAFIO: Construa um quadrado a partir de sua diagonal.
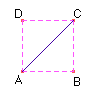
Resposta
4. Retângulo: é um polígono de quatro lados, com quatro ângulos retos.