As espirais podem ser originadas por equações em coordenadas polares.

Mas, o que são coordenadas polares?

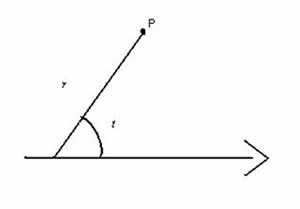
Iniciamos introduzindo o eixo polar: é uma semi-reta com origem em um ponto O, dito origem do sistema de coordenadas.

Com isto, podemos localizar qualquer ponto P do plano informando:

• a distância de P a O, que representamos por r;

• o ângulo que a semi-reta OP forma com o eixo polar, que representamos por t.

Feito isso, escrevemos P=(r, t) .

Parece complicado? Mas não é. As espirais possuem equações mais simples se usarmos coordenadas polares.

Uma família de espirais tem equação polar geral assim:

onde t é o ângulo e a e n constantes.

Em coordenadas cartesianas, essa família de espirais deve utilizar equações paramétricas. A forma geral das equações é :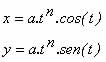

Cada espiral varia a e n. Vejamos as variações das espirais mais conhecidas:

Temos também a família da espiral logarítmica. Sua equação em coordenadas polares é:

e a equação cartesiana é: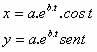

No Winplot, podemos fazer das duas maneiras. Em coordenadas polares, escolhemos a janela 2-d, depois equação e por último polar, e teremos este resultado:

E, para fazer em coordenadas cartesianas, o tipo de equação é paramétrica:

Um dos resultados será este:

Podemos, agora, explorar as espirais no Winplot.