utilizando repetidamente o menu 6 do Cabri Géomètre, pricipalmente,
a Translação (mosaico 1) e a Rotação (mosaico 2).
Você pode acompanhar, passo a passo a construção de ambos:
Mosaico 1
Primeiro, construímos um polígono regular, no exemplo, um quadrado.
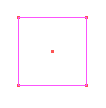
Depois, construímos um polígono qualquer, com um lado em comum ao quadrado.

Então, transladamos esta figura para a base oposta do quadrado.
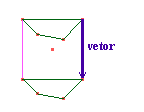
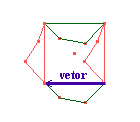
Fazemos o mesmo procedimento para o outro lado do quadrado e definimos então a peça final de nossa construção.
 |
 |
Contruímos, então, nosso mosaico através de translações da peça obtida.
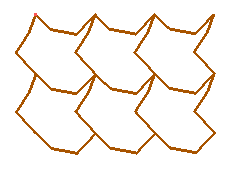
Observe como as peças se encaixam.
Neste mosaico o polígono regular que utilizamos é um hexágono.
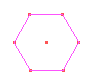
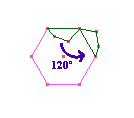
Desenhamos um polígono qualquer sobre um dos lados do hexágono e rotacionamos esta figura em torno de um dos vértices do hexágono com um ângulo de 120 graus, como mostra a figura abaixo.
Repetimos esse procedimento para os demais lados do hexágono e definimos a peça final.
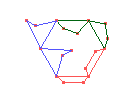 |
 |
Contruímos então nosso mosaico através de rotações da peça obtida.


