todos
primos !!
Nos perguntamos no entanto: Será que F5
também será um número primo?
Quem
respondeu a esta pergunta foi Leornard Euler (1707-1783), que em 1732,
provou que F5 é divisível por 641, e portanto
é um número composto 2_. Faça o teste em sua calculadora!
Dizemos então que indução matemática é uma ferramenta da qual os matemáticos se utilizam para demonstrar teoremas, a partir da observação de casos particulares.
Podemos observar, por exemplo, que a soma dos cubos dos 4 primeiros números inteiros é igual a um quadrado perfeito.

Nos perguntamos então:
Será que isto ocorrerá sempre ? Será que para a soma dos n primeiros números inteiros consecutivos teremos sempre como resultado um quadrado perfeito ?
Vamos testar agora para n=5 e n=6:

Observamos que aparentemente isto ocorrerá sempre. Mas ainda nada podemos afirmar. Antes vejamos que outras relações que encontramos no nosso exemplo.

Observamos que os quadrados perfeitos são na verdade a soma de uma progressão aritmética de razão 1. Somos assim, levados a formular uma conjectura bem geral:


O resultado que obtivemos apesar de ser bem interessante, é experimental e por isso não podemos assumí-lo como verdadeiro. Precisamos de uma demonstração rigorosa, matemática.
É muito provável que esta fórmula seja verdadeira para qualquer valor de n. Por mais que testemos inúmeros valores para n, mas sempre poderemos nos perguntar: Será que ela ainda será válida para o valor seguinte, (n+1) ?
Supondo que a fórmula valha para qualquer n, vamos testar se valerá para n+1 ! Teremos então:
 E ...
E ...
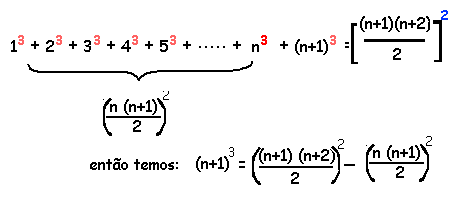
Fazendo um pouco de álgebra verificamos que esta expressão é realmente verdadeira. Mas não sabemos ainda se a nossa expressão inicial é verdadeira.
Mas sabemos que se somarmos à ela o termo n+1, em ambos os lados, chegaremos a uma expressão, que já mostramos, é verdadeira. Isto equivale a dizer que para n+1 a nossa expressão original é verdadeira.
Mas, já sabemos de antemão, pois testamos, que é verdadeira para n=6. E, como acabamos de ver que sempre valerá para o número seguinte, podemos dizer que valerá para n=7; sendo verdadeiro para n=7 podemos afirmar que valerá para n=8, e assim por diante.
|