State Estimation for Generalized First-Order Systems

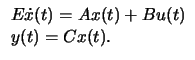
Many practical applications give rise to state-space systems of the form

$$\begin{array}{l} E \dot{x}(t) = A x(t) + B u(t) \\ y(t) = C x(t) . \end{array}$$

Here $E, A \in {\mathbb{R}}^{n \times n}$, $B \in {\mathbb{R}}^{n \times m}$ , $C \in {\mathbb{R}}^{r \times n}$, and $rank(E) \geq n-r$.

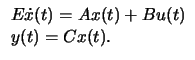
Once more, the state feedback control law

$$u(t) = v(t) - K x(t)$$

is considered. Feeding this information back into the system gives the closed-loop system

$$\begin{array}{ll} E \dot{x}(t) = (A - B K) x(t) + B v(t) \\ y(t) = C x(t) . \end{array}$$

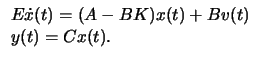
The concepts of controllability and observability of the system can be defined in terms of the associated standard state-space system.

The analogue of the Sylvester-observer equation for the generalized system is

$$X A - F X E = G C$$

where $$E , A \in {\mathbb{R}}^{n \times n}$$ and $C \in {\mathbb{R}}^{r \times n}$ are given and the matrices $$X \in {\mathbb{R}}^{s \times n}, F \in {\mathbb{R}}^{s \times s}$$, and $$G \in {\mathbb{R}}^{s \times r}$$ are to be found. Last equation will be referred to, by analogy, as the generalized Sylvester-observer equation.

The Luenberger-observer for the generalized system is the same as that of the standard system. That is, it is given by a system of differential equations

$$\dot{z}(t) = Fz(t) + Gy(t) + X B u(t)$$

where any initial condition $z(0)=z_0$ can be taken.

It can be shown that, if $F$ is a stable matrix, then $e(t) = z(t) - X E x(t)$ approaches zero as time $t$ increases.

If a full-order observer is constructed ($s=n$), then an estimate $\hat{x}(t)$ to the state vector $x(t)$ is obtained by solving the system

$$X E \hat{x}(t) = z(t)$$

once a solution $z(t)$ is computed.

However, if a reduced-order observer is constructed ($s=n-r$), an estimate $\hat{x}(t)$ of the state vector $x(t)$ is obtained by solving the system

$$\left[ \begin{array}{c} X E \\ C \end{array} \right] \hat{x}(t) = \left[ \begin{array}{c} z(t) \\ y(t) \end{array} \right].$$