Controle de Vibrações

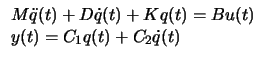
O problema de controle de vibrações busca melhorar a performance de sistemas vibratórios governados por um conjunto de equações diferenciais (normalmente parciais) que após serem discretizadas dão origem a um sistema da forma

$$\begin{array}{l} M \ddot{q}(t) + D \dot{q}(t) + K q(t) = B u(t) \\ y(t) = C_1 q(t) + C_2 \dot{q}(t) \end{array}$$

onde $M, D, K \in {\mathbb{R}}^{n \times n}$ , $B \in {\mathbb{R}}^{n \times m}$, e $C_1$, $C_2 \in {\mathbb{R}}^{r \times n}$.

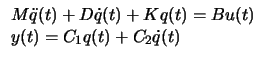
As matrizes $M, D$, e $K$, que são normalmente simétricas, são chamadas respectivamente, matrizes de massa, amortecimento, e rigidez. Além disso, $q(t)$, $\dot{q}(t)$, e $\ddot{q}(t)$ são , respectivamente, os vetores de deslocamento, velocidade, e aceleração .

Em estruturas de vibração tais como pontes, prédios, automóveis, aviões e naves espaciais, a performance é melhorada através da aplicação de uma lei de controle por realimentação de estado

$$u(t) = v(t) + K_1 q(t) + K_2 \dot{q}(t)$$.

Aqui $K_1, K_2 \in {\mathbb{R}}^{m \times n}$ são matrizes que são calculadas, pelo projetista da respectiva planta, de maneira que certos critérios de performance sejam atingidos. O vetor $v(t)$ representa as ações de controle que são externas à planta.

Quando a lei de controle acima é aplicada, a comportamento da planta é dado pelo comportamento do sistema de controle em laço fechado (closed-loop)

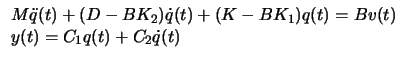$$\begin{array}{ll} M \ddot{q}(t) + (D - B K_2) \dot{q}(t) + (K - B K_1) q(t) = B v(t) \\ y(t) = C_1 q(t) + C_2 \dot{q}(t) \end{array}$$ .