Estudo de Caso:
aumento da exatidão na avaliação de ![]() via Série de Taylor
via Série de Taylor
Ao computador, a exponencial de um número real ![]() pode ser calculada
através de sua série ou expansão de Taylor:
pode ser calculada
através de sua série ou expansão de Taylor:

Escolhemos ![]() , por simplicidade (para que conheçamos a resposta
exata
, por simplicidade (para que conheçamos a resposta
exata ![]() ). Os termos parciais
). Os termos parciais
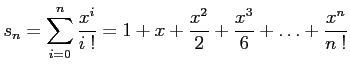
![]() sn = 1; nmax = 8; z=1; x = log(5); // comentario: exp(x)=5 //
sn = 1; nmax = 8; z=1; x = log(5); // comentario: exp(x)=5 //
![]() format("v",16)
format("v",16)
![]() for n=1:nmax
for n=1:nmax
![]() z = x*z/n; sn = sn + z;[n sn abs(sn-5)]
z = x*z/n; sn = sn + z;[n sn abs(sn-5)]
![]() end
end
Sendo
![]() , a tabela abaixo mostra como
evolui a exatidão das aproximações ao valor exato
, a tabela abaixo mostra como
evolui a exatidão das aproximações ao valor exato ![]() ,
quando a medida inteira da exatidão (d.s.e) é utilizada, e
quando a medida contínua da exatidão (digse) é utilizada.
,
quando a medida inteira da exatidão (d.s.e) é utilizada, e
quando a medida contínua da exatidão (digse) é utilizada.
| erro abs | d.s.e. | |||
| 1 | 2.609437912434101 | 2.39 | 0 | 0.019 |
| 2 | 3.904583109424218 | 1.09 | 0 | 0.358 |
| 3 | 4.599401703471827 | 0.40 | 1 | 0.796 |
| 4 | 4.878968550352922 | 0.12 | 1 | 1.315 |
| 5 | 4.968957646838940 | 0.031 | 2 | 1.906 |
| 6 | 4.993096290770655 | 0.0069 | 2 | 2.556 |
| 7 | 4.998646240584719 | 0.00135 | 3 | 3.267 |
| 8 | 4.999762778040077 | 0.00023 | 4 | 4.022 |
Teorema: relação entre a medida digse e a medida d.s.e
A medida em digse não difere da medida em d.s.e (dígitos significativos exatos) mais do que 1 unidade, para mais ou para menos.
Demonstração: seja
![]() .
.
O ![]() -ésimo algarismo (depois do ponto decimal) de uma aproximação
-ésimo algarismo (depois do ponto decimal) de uma aproximação
![]() de
de ![]() é o último correto se e somente se
é o último correto se e somente se
Sendo ![]() a medida da exatidão em digses, sabemos que
a medida da exatidão em digses, sabemos que
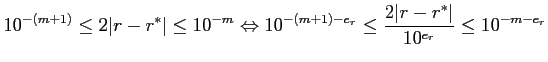
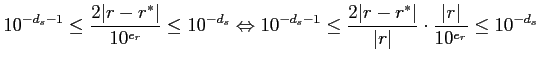
| (4) |
| (5) |
A primeira desigualdade, combinada com ![]() , implica
, implica
![]() . A segunda desigualdade, combinada com
. A segunda desigualdade, combinada com ![]() , implica
, implica
![]() . Dessa forma segue que
. Dessa forma segue que
![]() , conforme queríamos mostrar.
, conforme queríamos mostrar.