Mat01099 - Seminário Integrador III - UFRGS

Prof. João Batista Carvalho

Exponencial Matricial: definição, propriedades e aplicações

Ref: [1]: David Luenberger. Introduction to Dynamic Systems: Theory, Models and Applications, John Wiley and Sons, Inc. New York, 1979.

Def.: seja $A \in {\mathbb{R}}^{n \times n}$ uma matriz diagonalizável, onde

$$A = X \Lambda X^{-1} \ , \ \Lambda=diag(\lambda_1,\lambda_2,\dots,\lambda_n), X \mbox{ não singular}$$

e seja $f: {\mathbb{C}}\rightarrow {\mathbb{C}}$, $f(z) = e^z$, onde $z = u + iv$, $i^2= -1$ e

$$e^{u+iv} = e^u \cdot e^{iv} = e^u( \cos(v) + i\mbox{sen} \, (v))$$.

Definimos a exponencial matricial de $A$ via

$$e^{A} = X \left[ \begin{array}{cccc} e^{\lambda_1} & & & \\ & e... ...a_2} & & \\ & & \dots & \\ & & & e^{\lambda_n} \end{array} \right] X^{-1}$$

Além disso, lembramos da expansão de Taylor para $f(z) = e^z$:

$$f(z) = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \frac{z^4}{4!} + \dots$$

(disciplina futura Métodos IV), e então

$$e^A = X \left[ \begin{array}{cccc} \displaystyle \sum_{k=0}^{\inf... ...aystyle \sum_{k=0}^{\infty} \frac{\lambda_n^k}{k!} \end{array} \right] X^{-1}$$

o que implica

$$e^A = X [ I + \Lambda + \frac{\Lambda^2}{2!} + \frac{\Lambda^3}{3... ...c{A^2}{2!} + \frac{A^3}{3!} + \frac{A^4}{4!} + \dots + \frac{A^k}{k!} + \dots$$

Assim:, podemos definir $e^A$, para matrizes $A \in {\mathbb{R}}^{n \times n}$ quaisquer (não necessariamente diagonalizáveis) usando a expressão acima, que pode-se mostrar que é sempre convergente.

Propriedades de $e^A$:

(i)

$e^0 = I$;

(ii)

$e^A$ sempre comuta com a matriz $A$;

(iii)

$e^{A+B} = e^A e^B$;

(iv)

$e^{-A} = [e^A]^{-1}$ (matriz inversa);

(v)

se $\lambda \in {\mathbb{C}}$ é autovalor de uma matriz $A$i, com autovetor associado $x \neq 0$, então $e^{\lambda}$ é autovetor da matriz $e^A$, com o mesmo autovetor $x$.

Aplicação: solução de sistemas autônomos de equações diferenciais de primeira ordem

Considere um sistema de equações diferenciais de primeira ordem e coeficientes constantes

$$\left\{ \begin{array}{l} \dot{u}_1 = a_{11} u_1 + a_{12} u_2 + \d... ... \dot{u}_n = a_{n1} u_1 + a_{n2} u_2 + \dots + a_{nn} u_n \end{array} \right.$$

onde o ponto denota derivação no tempo $t$, com valores iniciais $$u_1(0), u_2(0), \dots, u_n(0)$$ dados. Na forma matricial, escrevemos

$$\left\{ \begin{array}{l} \displaystyle \frac{ d u(t)}{dt} = A u(t) \\ u(0) = u_0 \end{array} \right.$$

Resultado: a solução $u(t)$ do sistema acima satisfaz

$$u(t) = e^{A t} u_0 , t \geq 0$$

Justificativa:

$$\frac{ d e^{At }}{dt} = \frac{d}{dt} \left[ I + At + \frac{A^2t^2... ...2!} + 3\frac{A^3 t^2}{3!} + 4 \frac{A^4 t^3}{4!} + 5 \frac{A^5t^4}{5!} + \dots$$

$$A + \frac{A^2t}{1!} + \frac{A^3 t^2}{2!} + \frac{A^4 t^3}{3!} ... ...2t^2}{2!} + \frac{A^3 t^3}{3!} + \frac{A^4 t^4}{4!} + \dots \right] = A e^{At}$$

Dessa forma $u(0) = e^{0} u_0 = u_0$, e

$$\frac{ d u(t)}{dt} = \frac{ d e^{At} u_0} {dt} = A e^{At} u_0 = A u(t)$$.

Exemplo: Exemplo 2, seção 4.6 de [1],

$$\frac{d^2 x}{dt^2} = -w^2 x$$

com valores $w = \pi, x(0)=1, \dot{x}(0)=-1$. Mudanca de variavel: $u_1 = x, u_2 = \dot{x}$ conduz a

$\dot{u}_1 = \dot{x}=u_2$; $\dot{u}_2 = \ddot{x} = -w^2 x = - w^2 u_1$

e assim

$$\left[ \begin{array}{c} \dot{u}_1 \\ \dot{u}_2 \end{array} \right... ...end{array} \right] = A \left[ \begin{array}{c} u_1 \\ u_2 \end{array} \right]$$

Assim, no ambiente Scilab, usando expm, podemos encontrar a solução numérica via

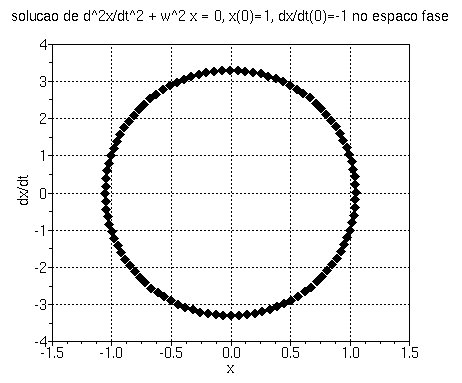
-->w=%pi; A = [0 1;-w*w 0], u0=[1;-1]
-->for t=0:.02:8
-->  ut=expm(A*t)*u0; plot2d( ut(1),ut(2),-4);
-->end
-->xgrid
-->xlabel('x'),ylabel('dx/dt')
-->title('solucao de d^2x/dt^2 + w^2 x = 0, x(0)=1, dx/dt(0)=-1 no espaco fase')

o que produz o gráfico abaixo: