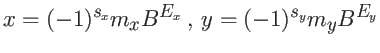
Como podemos dividir usando somas e produtos
Objetivo: em máquinas digitais, as operações de soma e produto de números, em aritmética ponto-flutuante, são implementadas em hardware. Todas as outras operações numéricas, incluindo a própria divisão ponto-flutuante, devem ser implementadas usando somas e produtos. Desenvolveremos fundamentação matemática para a divisão usando somas e produtos.
Imaginando o contexto de um sistema ponto-flutuante generalizado FL(B,p,L,U), em que números reais são representados na forma normalizada, sejam dois números
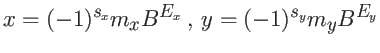
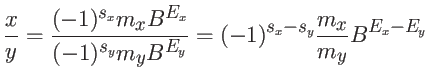
Estratégia colegial:
Um método que pode ser usado para calcular o inverso de um número
![]() dado é escrever
dado é escrever
![]() como
como
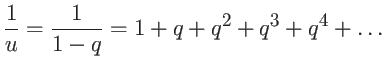
Exercício: calcular a divisão ponto-flutuante ![]() .
.
Temos ![]() ,
, ![]() ,
, ![]() ,
, ![]() e então
e então
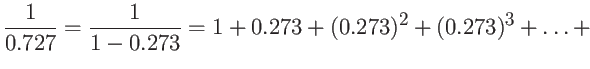
|
|
|
|
|
| 0 | 1. | 7 | 1.3754734 |
| 1 | 1.273 | 8 | 1.3755042 |
| 2 | 1.347529 | 9 | 1.3755127 |
| 3 | 1.3678754 | 10 | 1.375515 |
| 4 | 1.37343 | 11 | 1.3755156 |
| 5 | 1.3749464 | 12 | 1.3755158 |
| 6 | 1.3753604 | 13 | 1.3755158 |

Estratégia oficial: observamos que ![]() , o inverso
multiplicativo de
, o inverso
multiplicativo de ![]() , satisfaz o problema de raízes
, satisfaz o problema de raízes
![]() . A aplicação do Método de Newton
então produz
. A aplicação do Método de Newton
então produz
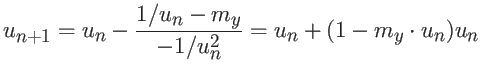 .
.
Escolhemos ![]() e menor que o valor exato de
e menor que o valor exato de
![]() , para que então
, para que então ![]() e
e
![]() , e a
convergência esteja garantida pelo Critério de Fourier.
, e a
convergência esteja garantida pelo Critério de Fourier.
Por outro lado, se ![]() , temos
, temos
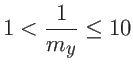
e então é seguro usar ![]() .
.
Exercício: calcular a divisão ponto-flutuante ![]() .
.
Temos ![]() ,
, ![]() ,
, ![]() ,
, ![]() . A sequência
NR é
. A sequência
NR é
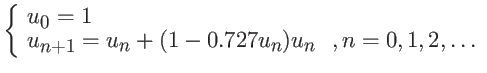
|
|
|
|
|
| 0 | 1 | 3 | 1.3754734 |
| 1 | 1.273 | 4 | 1.3755158 |
| 2 | 1.3678754 | 5 | 1.3755158 |
