Exercício 1 : Modelagem da periodicidade usando funções trigonométricas.
PEDE-SE encontrar uma
função ![]() que descreva a tabela
que descreva a tabela
|
|
0 | 1 | 2 | 4 | 5 | 6 | 8 | 9 | 10 | 12 |
|
|
1.2 | 2 | 1.6 | 1.2 | 2 | 1.6 | 1.2 | 2 | 1.6 | 1.2 |
Solução: Como os dados exibem periodicidade, sabemos que ![]() deve
ser uma função periódica. Lembramos que o menor período de uma
função
deve
ser uma função periódica. Lembramos que o menor período de uma
função ![]() é um
é um ![]() positivo tal que
positivo tal que ![]() para todo
para todo ![]() no
domínio de
no
domínio de ![]() .
Nossa tabela revela um menor período 4.
Por outro lado, uma função períodica bastante simples é um seno, ou uma
senóide.
Na disciplina de Cálculo, você teve contato com a idéia
de que alguns parâmetros, quando adicionados a uma função, provocam
certas alterações em seu gráfico, como
.
Nossa tabela revela um menor período 4.
Por outro lado, uma função períodica bastante simples é um seno, ou uma
senóide.
Na disciplina de Cálculo, você teve contato com a idéia
de que alguns parâmetros, quando adicionados a uma função, provocam
certas alterações em seu gráfico, como
| parâmetro | em matematica | em fisica |
|
|
translação vertical | normalmente considera |
|
|
translação horizontal | deslocamento de fase |
|
|
escala vertical | amplitude |
|
|
escala horizontal | velocidade |
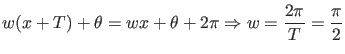
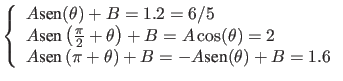
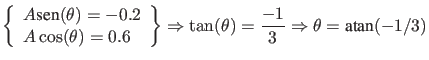
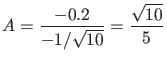 , o que implica
, o que implica
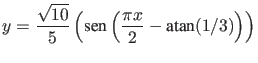
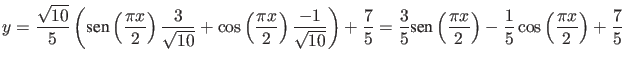 .
.
A figura abaixo mostra a curva acima, juntamente com os pontos da tabela. O gráfico foi gerado em MATLAB.
