Para resolver uma equação diferencial ordinária linear homogênea de 2
| (1) |
nosso procedimento usual tem sido o de, em primeiro lugar, encontrar duas soluções linearmente independentes
| (2) |
são soluções da EDO (1). Finalmente, argumentamos que, como a expressão (2) já envolve duas constantes arbitrárias, (2) é a solução geral de (1).
O procedimento descrito acima pode ser justificado rigorosamente, mas a justificativa para o fato de que a expressão (2) contém todas as soluções da EDO (1) envolve certos detalhes que estão em um nível acima do presente curso. O aluno que tenta entender o assunto, freqüentemente fica ainda em dúvida se não poderiam existir outras soluções além daquelas dadas por (2).
Apesar de que, para manter o nível deste curso, não podermos convencer o aluno com uma demonstração para o caso geral da equação (1), é perfeitamente possível dar uma demonstração simples e elementar para o caso particular das equações lineares homogêneas com coeficientes constantes, que cobre, por exemplo, as oscilações livres em um sistema massa-mola, ou em um circuito
Exempo 1. Consideremos a EDO
| (3) |
Sabemos que, para
| (4) |
é uma família de soluções de (3). Vamos agora provar que qualquer solução da EDO (3) está contida em (4). De fato, seja

O raciocínio acima pode ser empregado para qualquer EDO linear de coeficientes constantes.
Caso Genérico. Consideremos a EDO
| (5) |
Suponhamos que a equação característica tenha duas raízes diferentes, reais ou complexas,
 e
e 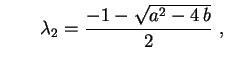
| (6) |
Substituindo
| (7) |
Também
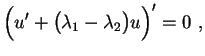 |
(8) |
ou seja,

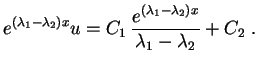
Caso de Raiz Dupla. Para completar o argumento, falta ainda considerar o caso em que a equação característica da EDO (1) tem raiz real dupla
Eduardo Brietzke