Para dar uma idéia do método das séries de potências
para resolver equações diferencias, vamos começar com um
exemplo.
Exemplo 1:
Consideremos a equação diferencial
Esta equação parece muito simples, no entanto os métodos de
resolução vistos na primeira área não se aplicam a ela. Vamos
procurar então uma solução expressa em forma de soma de uma
série de potências
Substituindo na equação, temos
No primeiro somatório, chamando 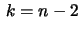 , temos
A seguir, em lugar da letra
, temos
A seguir, em lugar da letra 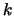 , podemos usar qualquer outra, inclusive
novamente
, podemos usar qualquer outra, inclusive
novamente 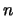 . Podemos também fazer o segundo somatório começar
de
. Podemos também fazer o segundo somatório começar
de 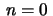 , pois fazer isto corresponde acrescentar uma parcela a mais
no somatório, mas esta parcela é nula. Obtemos, então,
Mudando a ordem dos termos e agrupando termos semelhantes, podemos
escrever na forma de um único somatório
Desta igualdade decorre que todos os coeficientes se anulam,
ou seja,
, pois fazer isto corresponde acrescentar uma parcela a mais
no somatório, mas esta parcela é nula. Obtemos, então,
Mudando a ordem dos termos e agrupando termos semelhantes, podemos
escrever na forma de um único somatório
Desta igualdade decorre que todos os coeficientes se anulam,
ou seja,
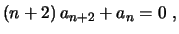
para
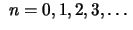
Chamamos esta última igualdade de fórmula recorrência.
Ela não nos diz nada sobre 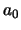 e
e 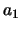 , mas a partir daí todos
os
, mas a partir daí todos
os 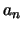 ficam determinados. Assim,
ficam determinados. Assim, 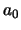 e
e 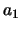 podem ser escolhidos
arbitrariamente, mas usando a fórmula de recorrência repetidas vezes,
vamos obtendo
Encontramos assim a solução da equação expressa na forma
podem ser escolhidos
arbitrariamente, mas usando a fórmula de recorrência repetidas vezes,
vamos obtendo
Encontramos assim a solução da equação expressa na forma
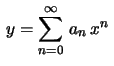 e dependendo de duas
constantes arbitrárias,
e dependendo de duas
constantes arbitrárias, 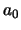 e
e 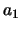 , o que não é de se estranhar,
já que se trata de uma equação de ordem 2.
, o que não é de se estranhar,
já que se trata de uma equação de ordem 2.
Escolhendo 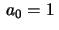 e
e 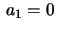 , obtemos
, obtemos
e
Encontramos, assim, uma solução da equação diferencial,
Observe que esta primeira solução poderia ser expressa em termos
das funções elementares. De fato, usando a série da exponencial,
obtemos
Escolhendo 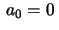 e
e 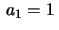 , obtemos
, obtemos
e
O símbolo  acima é chamado de fatorial duplo e indica o produto em
que os fatores vão diminuindo de 2 em 2 unidades. Assim, uma segunda
solução, linearmente independente da primeira, é dada por
Para verificar que de fato
acima é chamado de fatorial duplo e indica o produto em
que os fatores vão diminuindo de 2 em 2 unidades. Assim, uma segunda
solução, linearmente independente da primeira, é dada por
Para verificar que de fato 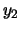 acima define uma solução da
equação diferencial é necessário, antes de mais nada, verificar
que a série converge, isto é, que a série de potências que
define
acima define uma solução da
equação diferencial é necessário, antes de mais nada, verificar
que a série converge, isto é, que a série de potências que
define 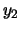 tem raio de convergência maior do que 0. Não faremos
isto aqui.
tem raio de convergência maior do que 0. Não faremos
isto aqui.
Observações: (i) Se
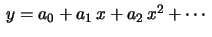 , então
, então
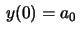 e
e
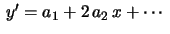 .
Logo
.
Logo
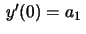 . Portanto nossa solução
. Portanto nossa solução 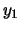 corresponde às
condições iniciais
corresponde às
condições iniciais
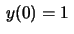 ,
,
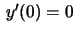 , enquanto que
, enquanto que
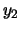 corresponde às condições inicias
corresponde às condições inicias
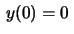 ,
,
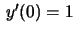 .
.
(ii) A solução encontrada
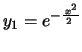 é uma função elementar. Usando nosso
método de encontrar uma segunda solução linearmente independente
para a equação linear homogênea:
é uma função elementar. Usando nosso
método de encontrar uma segunda solução linearmente independente
para a equação linear homogênea:
que nos dá
ou ainda,
Levando em conta que
de
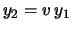
e
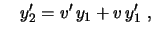
deduz-se que
Vamos então resolver o problema de valor inicial
Pondo 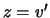 , a equação diferencial se reduz à equação de
primeira ordem
que é separável,
Da condição inicial
, a equação diferencial se reduz à equação de
primeira ordem
que é separável,
Da condição inicial
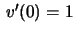 ou, equivalentemente,
ou, equivalentemente,
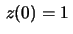 , segue que
, segue que 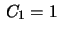 , isto é,
Logo
Usando que
, isto é,
Logo
Usando que
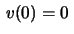 , obtemos, finalmente,
ou seja,
Temos, então, que
Conclusão:
, obtemos, finalmente,
ou seja,
Temos, então, que
Conclusão: 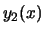 não se expressa em termos das funções
elementares. Ou seja, ao resolvermos uma equação diferencial
linear de coeficientes variáveis, pode acontecer que uma solução
não possa ser expressa em termos das funções elementares. Por
esta razão estamos buscando uma forma alternativa para expressar as
soluções, como soma de série de potências. Em outras palavras,
as funções elementares não constituem um universo suficientemente
grande para que com elas se possam expressar as soluções das
equações com coeficientes variáveis.
não se expressa em termos das funções
elementares. Ou seja, ao resolvermos uma equação diferencial
linear de coeficientes variáveis, pode acontecer que uma solução
não possa ser expressa em termos das funções elementares. Por
esta razão estamos buscando uma forma alternativa para expressar as
soluções, como soma de série de potências. Em outras palavras,
as funções elementares não constituem um universo suficientemente
grande para que com elas se possam expressar as soluções das
equações com coeficientes variáveis.
Exemplo 2: Consideremos o problema de valor inicial
Como as condições iniciais são dadas no ponto 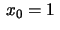 ,
procuramos a solução expressa em forma de série de potências
de
,
procuramos a solução expressa em forma de série de potências
de 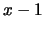 , pois se
então
, pois se
então
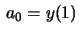 e
e
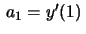 , de modo que as condições
iniciais do problema nos dizem que
, de modo que as condições
iniciais do problema nos dizem que 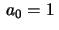 e
e
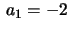 .
Substituindo na equação temos
Reescrevemos como
Fazendo mudança de índices, obtemos
Notando que o 1
.
Substituindo na equação temos
Reescrevemos como
Fazendo mudança de índices, obtemos
Notando que o 1 e 4
e 4 somatórios podem ser
começados em
somatórios podem ser
começados em 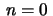 e o 3
e o 3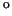 somatório pode ser
começado em
somatório pode ser
começado em 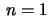 e agrupando os termos semelhantes, obtemos
finalmente
Para que a igualdade acima se cumpra é necessário que todos os
coeficientes da série se anulem. Obtemos, então,
e a fórmula de recorrência
Já tínhamos que
e agrupando os termos semelhantes, obtemos
finalmente
Para que a igualdade acima se cumpra é necessário que todos os
coeficientes da série se anulem. Obtemos, então,
e a fórmula de recorrência
Já tínhamos que 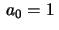 e
e
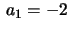 . Aplicando as fórmulas
acima, vamos encontrando, sucessivamente,
. Aplicando as fórmulas
acima, vamos encontrando, sucessivamente, 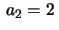 ,
,
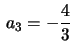 ,
,
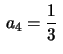 , etc. Obtemos então a expressão
, etc. Obtemos então a expressão
Observação: No exemplo 1 foi possível obter
uma fórmula geral para os coeficientes das soluções. Isto não
aconteceu no exemplo 2, onde é possível calcular tantos coeficientes
quanto se queira, mas não obtivemos uma fórmula geral para eles. Cabe
perguntar qual a causa desta diferença. A resposta é que no exemplo
1, a fórmula de recorrência
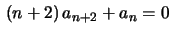 é do tipo
mais simples possível, envolve apenas dois termos. Assim, por
exemplo,
é do tipo
mais simples possível, envolve apenas dois termos. Assim, por
exemplo, 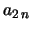 pode se expressar em função de
pode se expressar em função de 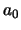 somente.
Isto não ocorre no exemplo 2, onde a fórmula de recorrência
somente.
Isto não ocorre no exemplo 2, onde a fórmula de recorrência
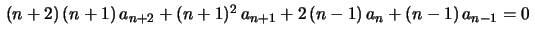 é mais complicada, envolvendo 4 termos. Em geral, só quando a
fórmula de recorrência envolve apenas 2 termos é que pode-se ter
esperança de encontrar uma expressão geral para os coeficientes.
é mais complicada, envolvendo 4 termos. Em geral, só quando a
fórmula de recorrência envolve apenas 2 termos é que pode-se ter
esperança de encontrar uma expressão geral para os coeficientes.
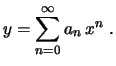
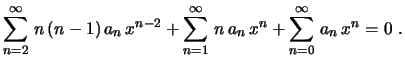
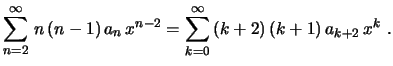
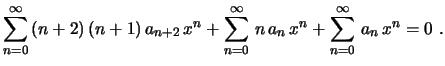
![$\displaystyle \sum_{n=0}^\infty\Bigl[(n+2)\,(n+1)\,a_{n+2}+(n+1)\,a_n\Bigr]x^n=0\ .
$](img10.gif)
 e dependendo de duas
constantes arbitrárias,
e dependendo de duas
constantes arbitrárias, ![]() e
e ![]() , obtemos
, obtemos
![]() e
e ![]() , obtemos
, obtemos
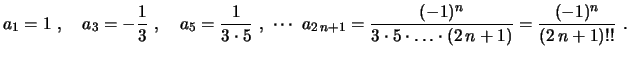
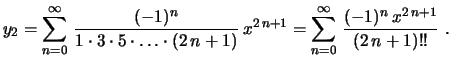
![]() , então
, então
![]() e
e
![]() .
Logo
.
Logo
![]() . Portanto nossa solução
. Portanto nossa solução ![]() corresponde às
condições iniciais
corresponde às
condições iniciais
![]() ,
,
![]() , enquanto que
, enquanto que
![]() corresponde às condições inicias
corresponde às condições inicias
![]() ,
,
![]() .
.
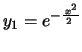 é uma função elementar. Usando nosso
método de encontrar uma segunda solução linearmente independente
para a equação linear homogênea:
é uma função elementar. Usando nosso
método de encontrar uma segunda solução linearmente independente
para a equação linear homogênea:
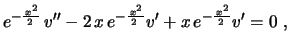
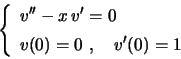
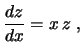
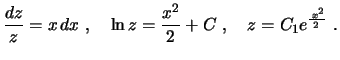
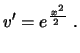
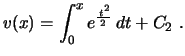
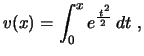
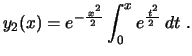
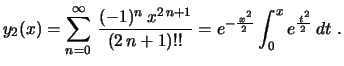
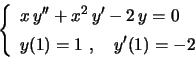
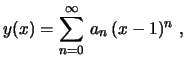
![$\displaystyle \bigl[(x-1)+1\bigr]\sum_{n=2}^\infty\,n\,(n-1)\,a_n\,(x-1)^{n-1}+
\bigl[(x-1)+1\bigr]^2\sum_{n=1}^\infty\,n\,a_n\,(x-1)^{n-1}-
\hspace{1.0cm}
$](img70.gif)

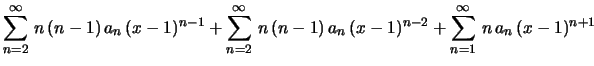
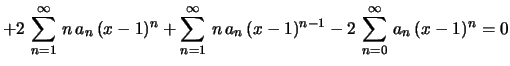
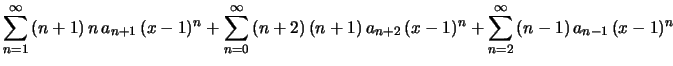
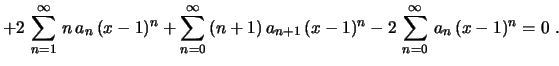
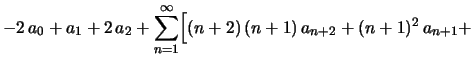
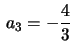 ,
,
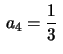 , etc. Obtemos então a expressão
, etc. Obtemos então a expressão
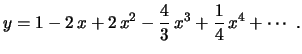
![]() é do tipo
mais simples possível, envolve apenas dois termos. Assim, por
exemplo,
é do tipo
mais simples possível, envolve apenas dois termos. Assim, por
exemplo, ![]() pode se expressar em função de
pode se expressar em função de ![]() somente.
Isto não ocorre no exemplo 2, onde a fórmula de recorrência
somente.
Isto não ocorre no exemplo 2, onde a fórmula de recorrência
![]() é mais complicada, envolvendo 4 termos. Em geral, só quando a
fórmula de recorrência envolve apenas 2 termos é que pode-se ter
esperança de encontrar uma expressão geral para os coeficientes.
é mais complicada, envolvendo 4 termos. Em geral, só quando a
fórmula de recorrência envolve apenas 2 termos é que pode-se ter
esperança de encontrar uma expressão geral para os coeficientes.