1. Campo Elétrico gerado por um Anel Circular
|
Consideremos uma carga elétrica com densidade
linear 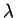 , uniformemente distribuída
sobre um anel circular de raio , uniformemente distribuída
sobre um anel circular de raio 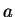 . Vamos
considerar o problema de calcular o potencial elétrico
em um ponto qualquer do espaço.
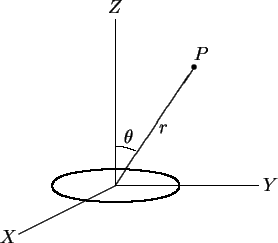
Suponhamos que tenha sido colocado um sistema de coordenadas
tendo a origen no centro do anel e o plano . Vamos
considerar o problema de calcular o potencial elétrico
em um ponto qualquer do espaço.
Suponhamos que tenha sido colocado um sistema de coordenadas
tendo a origen no centro do anel e o plano 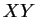 no
plano do anel e vamos usar coordenadas esféricas.
Antes de mais nada, observemos que, como a
distribuição
de cargas é simétrica em relação ao eixo no
plano do anel e vamos usar coordenadas esféricas.
Antes de mais nada, observemos que, como a
distribuição
de cargas é simétrica em relação ao eixo 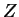 ,
o potencial elétrico resultante
vai ter esta mesma
simetria. ,
o potencial elétrico resultante
vai ter esta mesma
simetria.
|
Em outras palavras, vai ser uma
função 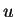 , dependendo apenas das
coordenadas esféricas
, dependendo apenas das
coordenadas esféricas 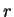 e
e 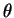 .
Vamos introduzir agora um método muito útil,
que pode ser aplicado em muitos problemas com este mesmo
tipo de simetria. A idéia é, numa primeira etapa,
resolver o problema muito mais simples de calcular o
potencial em um ponto
.
Vamos introduzir agora um método muito útil,
que pode ser aplicado em muitos problemas com este mesmo
tipo de simetria. A idéia é, numa primeira etapa,
resolver o problema muito mais simples de calcular o
potencial em um ponto
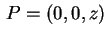 sobre o eixo
sobre o eixo 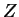 .
A seguir utiliza-se este resultado para obter o
potencial em um ponto qualquer do espaço.
.
A seguir utiliza-se este resultado para obter o
potencial em um ponto qualquer do espaço.
Segue daí, que a carga total sobre o anel gera no
ponto 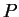 o potencial
Por exemplo, para
o potencial
Por exemplo, para
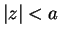 , desenvolvendo
pela série binomial, temos
Analogamente, para
, desenvolvendo
pela série binomial, temos
Analogamente, para
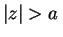 , temos
Agora que já temos a expressão do potencial sobre
os pontos do eixo dos
, temos
Agora que já temos a expressão do potencial sobre
os pontos do eixo dos  , é fácil obter sua
expressão em um ponto qualquer do espaço. Basta
lembrar que o potencial é uma função harmônica,
isto é, satisfaz a equação de Laplace
, é fácil obter sua
expressão em um ponto qualquer do espaço. Basta
lembrar que o potencial é uma função harmônica,
isto é, satisfaz a equação de Laplace
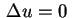 e usar o fato de que as funções
e usar o fato de que as funções
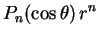
e
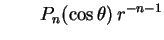
são harmônicas, valendo, respectivamente, 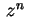 e
e
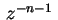 no ponto
no ponto
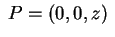 . Temos,
então, que
. Temos,
então, que
![$\displaystyle u(r,\theta)=
\frac{\lambda}{2\,\epsilon_0}\biggl[1-\frac{1}{2}\,\...
...5}{2\!\cdot\!4\!\cdot\!6}\,
\frac{r^6}{a^6}P_6(\cos\theta)+\cdots\biggr] \ ,
\ $](img30.gif)
se
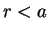
e
![$\displaystyle u(r,\theta)=
\frac{\lambda}{2\,\epsilon_0}\biggl[\frac{a}{r}-
\fr...
...}{2\!\cdot\!4\!\cdot\!6}\,\frac{a^7}{r^7}
P_6(\cos\theta)+\cdots
\biggr] \ ,
\ $](img32.gif)
se
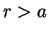
2. Potencial Gravitacional gerado por um Disco
Homogêneo
O primeiro passo é calcular o potencial nos pontos
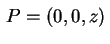 sobre o eixo
sobre o eixo 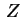 . Para
isto vejamos contribuição do anel formado pelos
pontos cuja distância à origem fica entre
. Para
isto vejamos contribuição do anel formado pelos
pontos cuja distância à origem fica entre
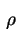 e
e
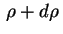 .
.
A distância de qualquer um destes
pontos ao ponto
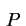 vale
vale
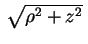 .
A área do anel vale .
A área do anel vale
![$ \,\pi\,\bigl[(\rho+d\rho)^2-\rho^2\bigr]\approx
2\,\pi\,\rho\,d\rho\,$](img51.gif) . Logo a massa do anel é,
aproximadamente, . Logo a massa do anel é,
aproximadamente,
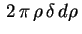 .
Portanto a contribuição
deste anel para o potencial
gravitacional no ponto .
Portanto a contribuição
deste anel para o potencial
gravitacional no ponto
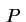 é é
|
|
Somando todas estas contribuições,
obtemos a expressão do potencial gravitacional gerado
no ponto 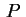 pelo disco todo
Calculando a integral obtemos
Para
pelo disco todo
Calculando a integral obtemos
Para
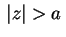 , tem-se
Usando a série binomial, obtém-se
O potencial que estamos buscando é uma função
harmônica e seus valores nos pontos
, tem-se
Usando a série binomial, obtém-se
O potencial que estamos buscando é uma função
harmônica e seus valores nos pontos
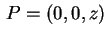 ,
com
,
com
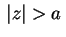 (esta condição garante
que a série converge), estão dados acima. Lembrando
que a função
é harmônica e coincide com
nos pontos
(esta condição garante
que a série converge), estão dados acima. Lembrando
que a função
é harmônica e coincide com
nos pontos
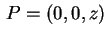 sobre o eixo
sobre o eixo 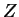 ,
concluímos que, para
,
concluímos que, para 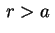 ,
Analogamente mostra-se que, para
,
Analogamente mostra-se que, para 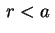 ,
,
Observações sobre o modelo físico.
O raciocínio feito para o potencial gravitacional seria
exatamente o mesmo para o caso de um potencial elétrico.
Do ponto de vista matemático, não há
diferença alguma. Ambos os campos são inversamente
proporcionais ao quadrado da distância. Apenas, do ponto de
vista físico, não é muito natural considerarar
uma distribuição homogênea de cargas elétricas
sobre um disco de material condutor. A carga não se distribuiria
de maneira homogênea sobre o disco e sim de
modo a tornar constante o potencial sobre o disco.
Com relação ao potencial gravitacional, poderíamos
pensar no disco como sendo o disco de uma galáxia, e, inclusive,
fazer os cálculos utilizando outras distribuições
de massa sobre este disco. Fica aqui a sugestão.

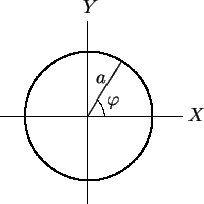
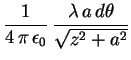
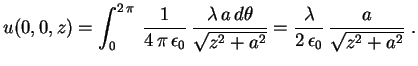
![$\displaystyle u(0,0,z)=\frac{\lambda}{2\,\epsilon_0}\,
\frac{1}{\displaystyle\s...
...{a^4}-
\frac{1\cdot3\cdot5}{2\cdot4\cdot6}\,\frac{z^6}{a^6}+\cdots
\biggr] \ .
$](img21.gif)
![$\displaystyle u(0,0,z)=\frac{\lambda}{2\,\epsilon_0}\,\frac{a}{z}\,
\frac{1}{\d...
...{z^5}-
\frac{1\cdot3\cdot5}{2\cdot4\cdot6}\,\frac{a^7}{z^7}+\cdots
\biggr] \ .
$](img23.gif)
![$\displaystyle u(r,\theta)=
\frac{\lambda}{2\,\epsilon_0}\biggl[1-\frac{1}{2}\,\...
...5}{2\!\cdot\!4\!\cdot\!6}\,
\frac{r^6}{a^6}P_6(\cos\theta)+\cdots\biggr] \ ,
\ $](img30.gif) se
se ![$\displaystyle u(r,\theta)=
\frac{\lambda}{2\,\epsilon_0}\biggl[\frac{a}{r}-
\fr...
...}{2\!\cdot\!4\!\cdot\!6}\,\frac{a^7}{r^7}
P_6(\cos\theta)+\cdots
\biggr] \ ,
\ $](img32.gif) se
se 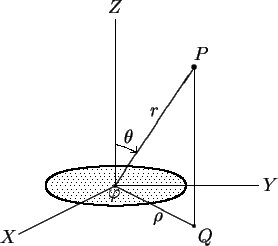
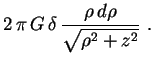

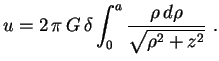
![$\displaystyle u(0,0,z)=2\,\pi\,G\,\delta\left.\sqrt{\rho^2+z^2}\,
\right\vert _{\rho=0}^{\rho=a}=2\,\pi\,G\,\delta\Bigl[\bigl(
a^2+z^2\bigr)^\frac12-z\Bigr]
$](img57.gif)
![$\displaystyle u(0,0,z)=2\,\pi\,G\,\delta\,z\biggl[\biggl(
1+\frac{a^2}{z^2}\biggr)^\frac12-1\biggr] \ .
$](img59.gif)
![$\displaystyle u(0,0,z)=2\,\pi\,G\,\delta\,z\biggl[\frac{1}{2}\,\frac{a^2}{z^2}-...
...frac{a^4}{z^4}+
\frac{1\cdot3}{2\cdot4\cdot6}\,\frac{a^6}{z^6}-
\cdots\biggr]
$](img60.gif)
![$\displaystyle =2\,\pi\,G\,\delta\biggl[\frac{1}{2}\,\frac{a^2}{z}-
\frac{1}{2\c...
...c{a^4}{z^3}+
\frac{1\cdot3}{2\cdot4\cdot6}\,\frac{a^6}{z^5}-
\cdots\biggr] \ .
$](img61.gif)
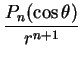
![$\displaystyle u=u(r,\theta,\varphi)=2\,\pi\,G\,\delta
\biggl[\frac{1}{2}\,\frac...
...!3}{2\!\cdot\!4\!\cdot\!6}\,
\frac{a^6P_5(\cos\theta)}{r^5}-
\cdots\biggr] \ .
$](img65.gif)
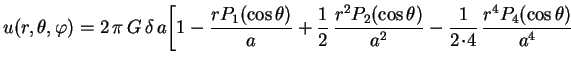
![$\displaystyle +\frac{1\!\cdot\!3}{2\!\cdot\!4\!\cdot\!6}\,
\frac{r^6P_6(\cos\theta)}{a^6}-
\cdots\biggr] \ .
$](img68.gif)