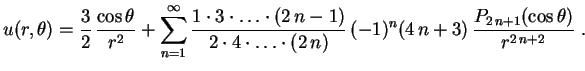Vamos usar os símbolos

|
Temos


|
em termos das coordenadas esféricas
Vamos usar os símbolospara indicar as coordenadas esféricas de um ponto.

Temos e também Nosso objetivo é expressar o laplaciano em 3 variáveis
Nosso objetivo é expressar o laplaciano em 3 variáveis

em termos das coordenadas esféricas. Um cálculo direto é bastante longo. Por isto seguimos outro caminho. Usando a expressão do laplaciano em 2 variáveis em termos das coordenadas polares, temos
 |
(1) |
Notemos que as relaçõessão análogas às relações entre as coordenadas cartesianas e polares no plano, somente, agora, com
e
desempenhando, respectivamente, os papéis de
e
. Portanto, usando novamente a expressão do laplaciano em cordenadas polares, podemos escrever
 |
(2) |
Somandoa ambos os lados em (1) temos
e, usando (2),
 |
(3) |
Precisamos expressarem coordenadas esféricas. Pela regra da cadeia
Em (1), estávamos mantendo
fixo e tomando
e
como variáveis independentes, de modo que
. Portanto
| (4) |
Desegue que
 |
(5) |
Por outro lado, de
 |
(6) |
segue que
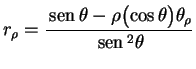 |
(7) |
Usando (5) e (6) em (7), obtém-se
| (8) |
Finalmente, substituindo (5) e (6) em (4), segue quee, portanto,
 |
(9) |
Finalmene, substituindo (9) em (3), obtemos
 |
(10) |
que é a expressão do laplaciano em coordenadas esféricas.
Simetria Axial
Vamos considerar somente problemas com simetria axial, isto é, o caso em que a funçãoindepende de
, dependendo apenas de
e
. As derivadas em relação a
se anulam e a expressão do laplaciano então se simplifica um pouco,
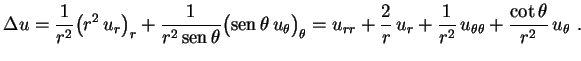 |
(11) |
Exemplo Dois hemisférios condutores de raio 1 são carregados até atingirem os potenciais dee
, respectivamente.
Como o potencial na esfera independe de

Determinar o potencial:
(a) Na região interior;
(b) Na região exterior.
Solução:
(a) Na região interior
, no
todo também vai independer, isto é, a solução
vai depender apenas de
e
. Temos, portanto, para
, o problema de Dirichlet
Resolvendo por separação de variáveis, iniciamos substituindo
na equação diferencial. Obtemos
Multiplicando por
e dividindo por
, separamos as variáveis
Seguem daí as duas equações diferenciais independentes Apesar de mais complicada, vamos começar resolvendo a segunda equação.
Apesar de mais complicada, vamos começar resolvendo a segunda equação.e

Este é um problema clássico, para o qual existe um método também clássico de resolução. Ele consiste em fazer a mudança de variável.
Substituindo na equação diferencial obtemos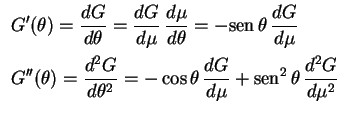 isto é,
isto é, que é a já estudada equação de Legendre. Como a variação de
que é a já estudada equação de Legendre. Como a variação de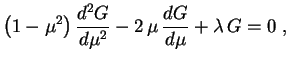
é no intervalo
, segue que
varia no intervalo
. Mas só nos servem soluções limitadas da equação de Legendre no intervalo
, soluções que sejam definidas e finitas para
. Como vimos acima, isto só acontece para
Substituindo este valor de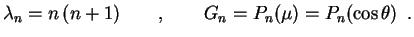
na outra equação, obtemos a equação de Euler-Cauchy
cuja solução geral é pois
pois
e
são as soluções da equação
.
Os cálculos que fizemos até aqui são válidos tanto para a região interior quanto exterior à esfera. Seriam válidos também para a região entre duas esferas centradas na origem.
Conclusão: Procurando pelo método de separação de variáveis, as funções da formasatisfazendo a equação de Laplace
, encontramos para cada

e

Neste ponto vamos começar a tratar especificamente o problema de Dirichlet para a região interior à esfera. Estamos procurando soluções definidas inclusive na origem, onde. Logo
, pois
se torna infinita na origem. Assim,
e, então, Fazendo a superposição, temos
Fazendo a superposição, temos As condições de fronteira
As condições de fronteira nos dizem que os
nos dizem que os
são os coeficientes da expansão
Sabemos que A integral acima foi calculada em um exercício da lista,
A integral acima foi calculada em um exercício da lista,
e
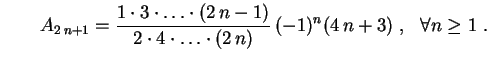 Logo, na região interior à esfera,
Logo, na região interior à esfera,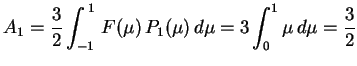
,

(b) Na região exterior
Passamos agora a considerar o problema de DirichletA solução é igual ao anterior, exceto que agora, para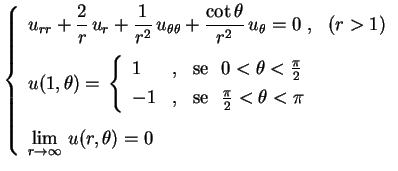 a condição
a condição
nos dá
, isto é,
A solução, então é,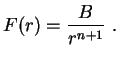 Como acima, obtemos
Como acima, obtemos Logo, na região exterior à esfera,
Logo, na região exterior à esfera,e

,