Ponto Singular Irregular — Exemplos
Recordemos que um ponto singular 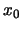 para a equação diferencial
é dito um ponto singular regular se
para a equação diferencial
é dito um ponto singular regular se

é analítica em
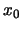
e
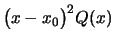
é analítica em
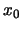
,
isto é, se a singularidade dos coeficientes  e
e
 pode ser removida pela multiplicação,
respectivamente, por
pode ser removida pela multiplicação,
respectivamente, por
 e
e
 .
.
Um ponto singular que não é regular é chamado de ponto
singular irregular. Para os pontos singulares regulares foi
desenvolvido o método de Frobenius. Vamos mostrar com exemplos
que no caso de ponto singular irregular pode não existir
solução em série de potências.
Exemplo 1. Consideremos a equação diferencial
 |
(1) |
próximo ao ponto  .
Trata-se de um ponto singular irregular. De fato, dividindo (1) por
.
Trata-se de um ponto singular irregular. De fato, dividindo (1) por
 , para reduzir a equação à forma
canônica, temos
, para reduzir a equação à forma
canônica, temos

e

de modo que a função  não é analítica no
ponto
não é analítica no
ponto  . Vamos procurar, como no método de Frobenius,
uma solução da forma
. Vamos procurar, como no método de Frobenius,
uma solução da forma
 |
(2) |
Substituindo em (1), temos
ou seja,
ou ainda,
Segue daí que
e também a fórmula de recorrência
Para  , a recorrência fica
Logo
, a recorrência fica
Logo
 |
(3) |
Aplicando (3) repetidas vezes, obtemos
Logo a solução deve ser
 |
(4) |
Acontece que a série de potências (4) tem raio de
convergência  , isto é, converge apenas para
, isto é, converge apenas para
 , não definindo, portanto, uma função. De fato, se
, não definindo, portanto, uma função. De fato, se
 , pelo teste da razão,
Pelo teste da razão, (4) diverge para todo
, pelo teste da razão,
Pelo teste da razão, (4) diverge para todo
 .
.
Conclusão: A equação diferencial (1)
não admite solução em forma de série (2).
Exemplo 2. Consideremos agora a equação
diferencial
 |
(5) |
 é um ponto singular irregular. Procurando
solução da forma (2), temos
Logo
Segue que
Obtém-se a equação
é um ponto singular irregular. Procurando
solução da forma (2), temos
Logo
Segue que
Obtém-se a equação
 |
(6) |
e a fórmula de recorrência
 |
(7) |
Substituindo a solução de (6)
em (7), obtém-se
 |
(8) |
É necessário distinguir 2 casos.
Caso 1:
 .
.
Neste caso o coeficiente de  em (8) nunca se
anula. Então
A solução é
em (8) nunca se
anula. Então
A solução é
 |
(9) |
Pelo teste da razão, a série (9) tem raio de convergência 0,
converge somente para  . De fato, se
. De fato, se
 , então
Pelo mesmo argumento do primeiro exemplo, neste caso a EDO (5)
não admite solução em forma de série (2).
, então
Pelo mesmo argumento do primeiro exemplo, neste caso a EDO (5)
não admite solução em forma de série (2).
Caso 2:
 .
.
Neste caso o coeficiente de  em (8) vai se
anular para um certo
em (8) vai se
anular para um certo  . Para fixar as idéias, digamos que
. Para fixar as idéias, digamos que
 . Vamos ter
. Vamos ter
 |
(10) |
Segue que
Para  , (10) fica
Logo
Para
, (10) fica
Logo
Para  , (10) nos diz
e, portanto,
Seguindo o argumento, obtemos
Neste caso temos uma solução em forma de série (2), o
polinômio
No caso (2) temos sempre uma solução polinomial.
, (10) nos diz
e, portanto,
Seguindo o argumento, obtemos
Neste caso temos uma solução em forma de série (2), o
polinômio
No caso (2) temos sempre uma solução polinomial.
Eduardo Brietzke
 e
e 



![$\displaystyle -ra_0x^r+\sum_{n=0}^\infty\biggl[\Bigr((n+r)(n+r+2)+1\Bigr)a_n-
\bigl(n+1+r\bigr)a_{n+1}\biggr]x^{n+r}=0 \ .
$](img18.gif)




![$\displaystyle \bigl(\alpha r+\beta\bigr)a_0x^r+\sum_{n=1}^\infty\Bigl[
\bigl(n+...
...)\bigl(n+r-2\bigr)a_{n-1}+
\Bigl(\alpha(n+r)+\beta\Bigr)a_n\Bigr]x^{n+r}=0 \ .
$](img33.gif)


 .
.



 .
.
 . Vamos ter
. Vamos ter

