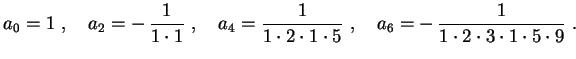Pontos Singulares Regulares - Método de Frobenius
Definição. Seja  um ponto singular
para a equação diferencial
Dizemos que
um ponto singular
para a equação diferencial
Dizemos que  é um ponto singular regular se
é um ponto singular regular se

é analítica em

e

é analítica em

,
isto é, se a singularidade dos coeficientes  e
e
 pode ser removida pela multiplicação,
respectivamente, por
pode ser removida pela multiplicação,
respectivamente, por
 e
e
 .
.
Exemplos.
1.  é um ponto singular
regular para a equação de Cauchy-Euler
é um ponto singular
regular para a equação de Cauchy-Euler
De fato, dividindo por  , para reduzir a equação à
forma canônica, temos
, para reduzir a equação à
forma canônica, temos
 e
e
 . As singularidades destas
funções podem ser removidas por multiplicação:
. As singularidades destas
funções podem ser removidas por multiplicação:

e
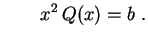
2.  é um ponto singular
regular para a equação de Bessel
é um ponto singular
regular para a equação de Bessel

parâmetro fixado

De fato, dividindo por  , temos
, temos

e

Multiplicando,
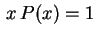 e
e
 são
analíticas em 0.
são
analíticas em 0.
OBS. O estudo que fizemos da equação de
Cauchy-Euler, nos mostra que existe solução da forma
 ,
,  não necessariamente inteiro. Concluímos
daí que no caso de ponto singular regular, não vamos
poder procurar solução na forma de uma série de
potências, pois séries de potências envolvem somente
potências de
não necessariamente inteiro. Concluímos
daí que no caso de ponto singular regular, não vamos
poder procurar solução na forma de uma série de
potências, pois séries de potências envolvem somente
potências de  com expoente inteiro. Vamos ter que procurar
a solução numa forma que contenha como caso particular as
funções
com expoente inteiro. Vamos ter que procurar
a solução numa forma que contenha como caso particular as
funções  .
.
Método de Frobenius. O Método de Frobenius
para uma equação com ponto singular regular, consiste em
procurar solução na forma
Podemos sempre supor
Basta escolher como  o menor expoente de
o menor expoente de  que aparece na
série solução. Se
que aparece na
série solução. Se  é o menor expoente presente, o
coeficiente
é o menor expoente presente, o
coeficiente 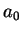 de
de  é não nulo. A partir daqui
vamos considerar sempre
é não nulo. A partir daqui
vamos considerar sempre
 . O caso geral pode ser sempre reduzido a este pela
mudança de variável
. O caso geral pode ser sempre reduzido a este pela
mudança de variável
 .
.
Exemplo 1.
 .
.
Substituímos

onde

Note que na derivada,
o índice obrigatoriamente começa a variar a partir de
 , e não a partir de
, e não a partir de 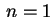 , pois como o primeiro termo de
, pois como o primeiro termo de
 em geral não é uma
constante, este não se anula por derivação. Não temos
aqui a liberdade de escolha de começar, conforme a
conveniência, a partir de
em geral não é uma
constante, este não se anula por derivação. Não temos
aqui a liberdade de escolha de começar, conforme a
conveniência, a partir de  ou de
ou de  , que
tínhamos no método de resolução por série de
potências em um ponto ordinário. A mesma observação vale
para a derivada de segunda ordem
Substituindo
, que
tínhamos no método de resolução por série de
potências em um ponto ordinário. A mesma observação vale
para a derivada de segunda ordem
Substituindo  ,
, 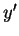 e
e  por suas expansões em série na
equação diferencial dada, obtemos
Agrupando os termos em
por suas expansões em série na
equação diferencial dada, obtemos
Agrupando os termos em  , obtemos
Fazendo
, obtemos
Fazendo  no segundo somatório,
No segundo somatório podemos substituir
no segundo somatório,
No segundo somatório podemos substituir  por qualquer letra,
inclusive
por qualquer letra,
inclusive 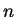 . Separamos os 2 primeiros termos do primeiro
somatório e combinamos os 2 somatórios restantes
Se quisermos obter uma série de potências, dividimos por
. Separamos os 2 primeiros termos do primeiro
somatório e combinamos os 2 somatórios restantes
Se quisermos obter uma série de potências, dividimos por
 . Portanto valem as mesmas observações feitas no
método de séries de potências e, então, o coeficiente
de cada
. Portanto valem as mesmas observações feitas no
método de séries de potências e, então, o coeficiente
de cada  deve se anular. Como
deve se anular. Como
 , temos
, temos
(i)
 , chamada de
equação indicial
, chamada de
equação indicial
(ii)

(iii)
 , para
, para
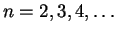
Esta última é a fórmula de recorrência.
A equação indicial (i) é uma equação
algébrica de grau 2. As suas raízes dão os possíveis
valores para  . No exemplo que estamos considerando a
equação indicial é
. No exemplo que estamos considerando a
equação indicial é
cujas raízes são

e

Por razões que vão ser importantes mais tarde, nos casos
mais complicados, é conveniente trabalhar primeiro com a maior
das raízes da equação indicial. Por esta razão
indicamos por  e
e  , respectivamente, a maior e a menor
das raízes da equação indicial.
, respectivamente, a maior e a menor
das raízes da equação indicial.
1
 Solução. Com
Solução. Com

A equação (ii) fica
Então 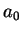 pode ser escolhido arbitrariamente, com a única
restrição que seja diferente de 0. Mas necessariamente
pode ser escolhido arbitrariamente, com a única
restrição que seja diferente de 0. Mas necessariamente
 . Escolhemos
. Escolhemos  .
.
A fórmula de recorrência fica
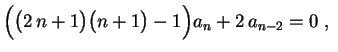
para

ou seja,
Segue que

para

Concluímos que
Simplificando, obtemos
Em geral,
Obtemos então a solução
Note que esta solução pode ser reescrita na forma de um
único somatório
2
 Solução. Com
Solução. Com

A equação (ii) fica
Ainda podemos escolher 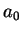 arbitrariamente, com a única
restrição que seja diferente de 0. Mas necessariamente
arbitrariamente, com a única
restrição que seja diferente de 0. Mas necessariamente
 . Escolhemos
. Escolhemos  .
.
A fórmula de recorrência fica
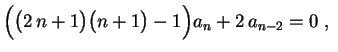
para

ou seja,
Segue que

para

Concluímos que
Simplificando, obtemos
Em geral,
Obtemos então a solução
Encontramos assim duas soluções linearmente independentes
para nosa equação diferencial linear homogênea. É
imediato que 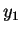 e
e 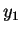 são linearmente independentes. Uma
delas não é múltiplo da outra, pois num caso a potência de
são linearmente independentes. Uma
delas não é múltiplo da outra, pois num caso a potência de
 de menor expoente que aparece é
de menor expoente que aparece é
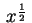 e no
outro caso é
e no
outro caso é
 .
.
Veremos que existem 3 casos diferentes no Método de Frobenius.
O exemplo dado acima é do caso mais simples, em que a
equação indicial em duas raízes distintas  e
e
 , mas cuja diferença
, mas cuja diferença  não é um inteiro.
Existe ainda um segundo caso, de raiz dupla
não é um inteiro.
Existe ainda um segundo caso, de raiz dupla
 , e um
terceiro caso, de raízes distintas
, e um
terceiro caso, de raízes distintas
 tais
que
tais
que
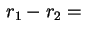 inteiro.
inteiro.
 e
e
 . As singularidades destas
funções podem ser removidas por multiplicação:
. As singularidades destas
funções podem ser removidas por multiplicação:
 e
e 
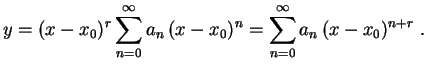
 onde
onde 



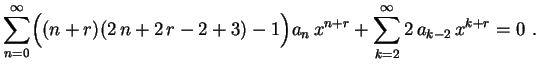

![$\displaystyle \hspace{3.0cm}
+\sum_{n=2}^\infty\biggl[\Bigl((n+r)(2\,n+2\,r+1)-1\Bigr)a_n+
2\,a_{n-2}\biggr]x^{n+r}=0
$](img53.gif)

 , para
, para
 e
e 
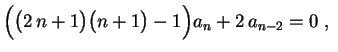 para
para  para
para 

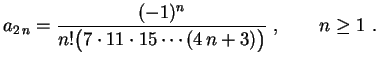


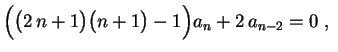 para
para  para
para