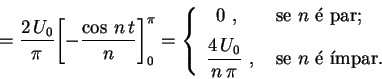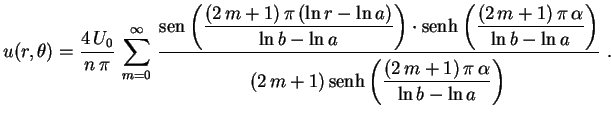EXEMPLO - Equação de Euler com
raízes complexas e apliacação a um problema
de Dirichlet
Sabemos que, para resolver a Equação de
Cauchy-Euler
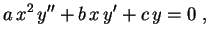 |
(1) |
devemos começar procurando uma solução da forma 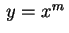 .
Substituindo em (1) vemos que
.
Substituindo em (1) vemos que 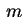 deve ser raiz da equação
algébrica
deve ser raiz da equação
algébrica
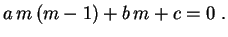 |
(2) |
Suponhamos que (2) tenha raízes complexas
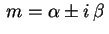 . Com elas construímos duas
soluções linearmente independentes de (1),
. Com elas construímos duas
soluções linearmente independentes de (1),
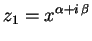
e
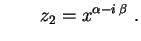
Já tínhamos trabalhado com exponenciais com expoente
complexo, mas de base 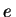 . É fácil dar um sentido às
exponenciais acima, cuja base não é
. É fácil dar um sentido às
exponenciais acima, cuja base não é 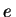 :
:
Analogamente obtemos
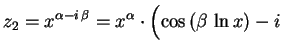
sen
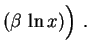
As duas soluções 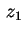 e
e 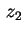 de (1) encontradas
acima são linearmente independentes mas assumem valores complexos,
o que pode ser um inconveniente para algumas aplicações. Por
esta razão, vamos preferir as combinações lineares delas
de (1) encontradas
acima são linearmente independentes mas assumem valores complexos,
o que pode ser um inconveniente para algumas aplicações. Por
esta razão, vamos preferir as combinações lineares delas
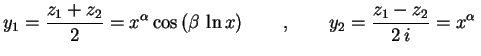
sen
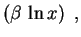
que são linearmente independentes e reais.
Aplicação (exercício 9 da lista 11).
Determine a temperatura estacionária
em uma barra, cuja seção é
Precisamenete, temos o problema de Dirichlet:
Resolvendo pelo método de separação de variáveis,
começamos procurando 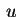 da forma
da forma
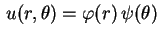 . Substituindo na
equação diferencial, temos
Multiplicando por
. Substituindo na
equação diferencial, temos
Multiplicando por 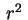 e dividindo por
e dividindo por
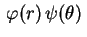 , obtém-se
Ficamos, então, com duas equações diferenciais
independentes:
, obtém-se
Ficamos, então, com duas equações diferenciais
independentes:
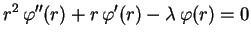
e
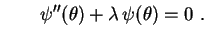
A primeira é uma equação de Cauchy-Euler e a segunda
é uma equação linear de coeficientes constantes.
A condição de fronteira
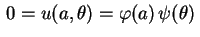 nos dá
nos dá
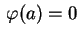 ,
pois caso contrário, teríamos
,
pois caso contrário, teríamos
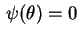 ,
para todo
,
para todo
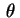 , que corresponde à solução
trivial
, que corresponde à solução
trivial 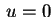 . Analogamente as condições de
fronteira
. Analogamente as condições de
fronteira
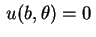 e
e
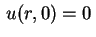 nos dão
nos dão
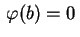 e
e
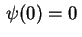 . Passemos
ao estudo do problema
1
. Passemos
ao estudo do problema
1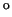 Caso:
Caso:
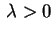
Neste caso,
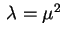 , com
, com 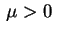 . A
equação algébrica
. A
equação algébrica
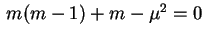 tem duas raízes reais
diferentes
tem duas raízes reais
diferentes
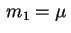 e
e
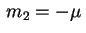 . Logo a
equação de Cauchy-Euler
tem solução
Aplicando as condições de fronteira, temos
Segue daí que
. Logo a
equação de Cauchy-Euler
tem solução
Aplicando as condições de fronteira, temos
Segue daí que 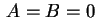 , pois
pois
, pois
pois 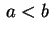 . Logo
. Logo
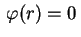 e a solução
é trivial.
e a solução
é trivial.
2 Caso:
Caso:
Neste caso, a solução da equação
de Euler
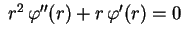 é
é
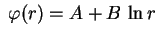 , pois a equação
algébrica
, pois a equação
algébrica
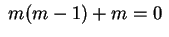 tem raiz dupla
tem raiz dupla
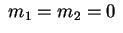 .
As condições de fronteira
.
As condições de fronteira
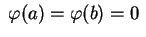 nos dão
nos dão 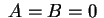 . Este caso, portanto, também
é trivial.
. Este caso, portanto, também
é trivial.
3 Caso:
Caso:
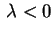
Neste caso,
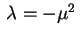 , com
, com 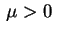 . A
equação algébrica
. A
equação algébrica
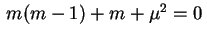 tem duas raízes imaginárias
tem duas raízes imaginárias
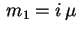 e
e
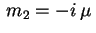 . Logo a
equação de Cauchy-Euler
tem solução
. Logo a
equação de Cauchy-Euler
tem solução
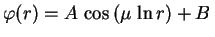 sen
sen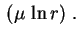
As condições de fronteira
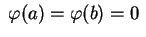 nos dão
Só teremos solução não trivial para nosso problema,
se o sistema acima possuir solução não trivial
para
nos dão
Só teremos solução não trivial para nosso problema,
se o sistema acima possuir solução não trivial
para 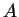 e
e 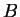 , mas isto só acontece se seu
determinante for nulo, isto é,
ou seja
Segue que devemos ter
ou seja,
Encontramos assim as funções
, mas isto só acontece se seu
determinante for nulo, isto é,
ou seja
Segue que devemos ter
ou seja,
Encontramos assim as funções
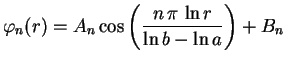 sen sen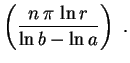 |
(3) |
Mas temos a condição
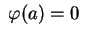 , dizendo que
, dizendo que
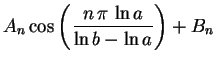 sen sen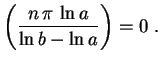 |
(4) |
Em (3) acima,
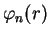 está expressa em termos de
duas constantes
está expressa em termos de
duas constantes 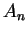 e
e 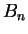 , mas, usando (4), podemos
eliminar uma constante.
, mas, usando (4), podemos
eliminar uma constante.
Multiplicando (3) por
 sen
sen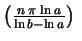 ,
obtemos
,
obtemos
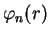
sen
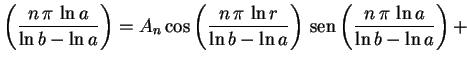
Usando (4), segue que
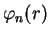
sen
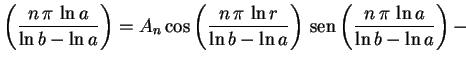

sen
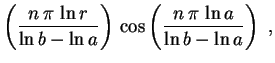
e, finalmente,
Analogamente, multiplicando (3) por
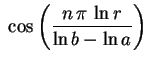 ,
obtém-se
,
obtém-se
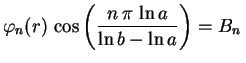 sen sen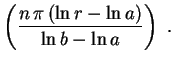 |
(6) |
Como
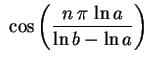 e
e
 sen
sen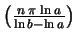 não podem ser ambos nulos,
segue de (5) e (6) que existe uma constante
não podem ser ambos nulos,
segue de (5) e (6) que existe uma constante 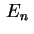 (igual a
(igual a
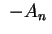 sen
sen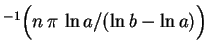 ou a
ou a
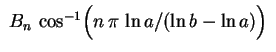 )
tal que
)
tal que
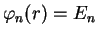
sen
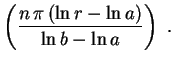
O valor de
 que corresponde a
que corresponde a
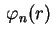 é
Pondo este valor de
é
Pondo este valor de
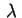 na outra equação, obtemos
cuja solução é
Usando a condição de fronteira
na outra equação, obtemos
cuja solução é
Usando a condição de fronteira
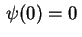 ,
obtemos
,
obtemos 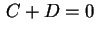 e, daí,
e, daí,
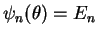
senh
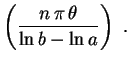
O terceiro caso nos dá, portanto,
Fazendo a superposição dos termos encontrados, obtemos
Finalmente, usando a condição
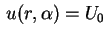 , temos
Observemos que a expansão acima não é uma série de
Fourier (na variável
, temos
Observemos que a expansão acima não é uma série de
Fourier (na variável 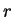 ), mas se converte em uma série de
Fourier pela mudança de variável
De fato, quando
), mas se converte em uma série de
Fourier pela mudança de variável
De fato, quando 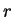 varia no intervalo
varia no intervalo 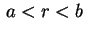 , vamos ter
, vamos ter
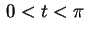 e
que é uma expansão em série de senos no intervalo
e
que é uma expansão em série de senos no intervalo
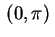 , para a função constante. Segue que
Finalmente, obtemos a resposta
, para a função constante. Segue que
Finalmente, obtemos a resposta
Eduardo H. M. Brietzke
![]()
![]() .
Substituindo em (1) vemos que
.
Substituindo em (1) vemos que ![]() deve ser raiz da equação
algébrica
deve ser raiz da equação
algébrica
![]()
![]() . Com elas construímos duas
soluções linearmente independentes de (1),
Já tínhamos trabalhado com exponenciais com expoente
complexo, mas de base
. Com elas construímos duas
soluções linearmente independentes de (1),
Já tínhamos trabalhado com exponenciais com expoente
complexo, mas de base ![]() e
e ![]()
![]() . É fácil dar um sentido às
exponenciais acima, cuja base não é
. É fácil dar um sentido às
exponenciais acima, cuja base não é ![]() :
:
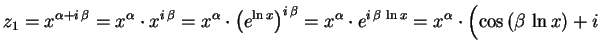 sen
sen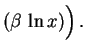
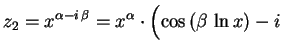 sen
sen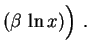
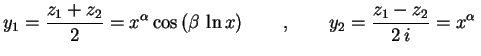 sen
sen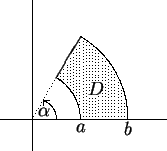
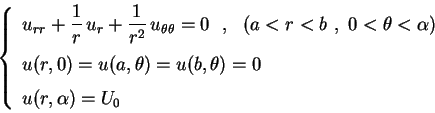
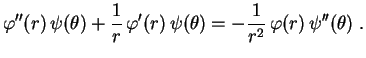
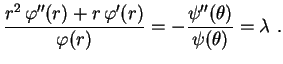
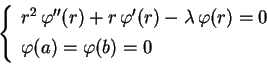
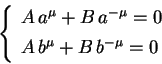
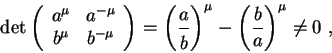
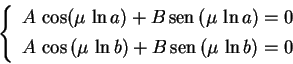
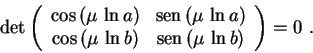
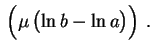
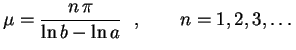
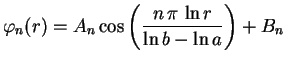 sen
sen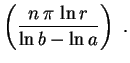
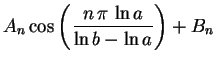 sen
sen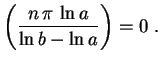
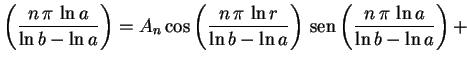
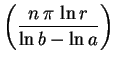 sen
sen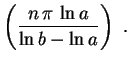
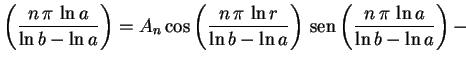
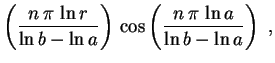
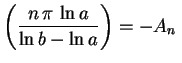 sen
sen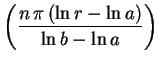
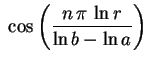 ,
obtém-se
,
obtém-se
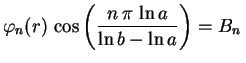 sen
sen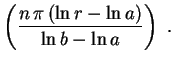
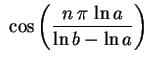 e
e
 ou a
ou a
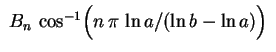 )
tal que
)
tal que
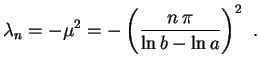
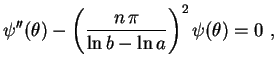
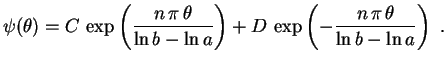
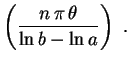
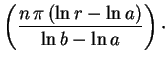 senh
senh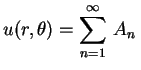 sen
sen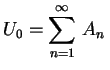 sen
sen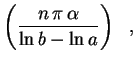 para todo
para todo 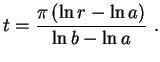
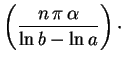 sen
sen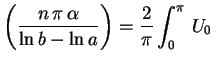 sen
sen