Consideremos o problema de determinar qual a
forma que deve ter um espelho para que tenha a propriedade
que, quando um feixe de raios paralelos incidir sobre o
espelho, os raios refletidos se concentrem em um único
ponto  , o foco do espelho.
Este é o tipo de espelho que deve ser usado em um
telescópio, a fim de produzir uma imagem perfeita.
Outra situação em que este espelho é
usado é em uma antena parabólica (veremos que esta
deve ser a forma do espelho). Invertendo o sentido de
percurso dos raios, o mesmo tipo de situação
se apresenta quando emitimos um sinal, a partir
de ponto
, o foco do espelho.
Este é o tipo de espelho que deve ser usado em um
telescópio, a fim de produzir uma imagem perfeita.
Outra situação em que este espelho é
usado é em uma antena parabólica (veremos que esta
deve ser a forma do espelho). Invertendo o sentido de
percurso dos raios, o mesmo tipo de situação
se apresenta quando emitimos um sinal, a partir
de ponto  , e desejamos que este sinal seja captado
em um outro ponto, a grande distância. Fazemos com que
ele seja refletido por um anteparo. A fim de que o sinal
possa ser captado facilmente, não queremos que ele perca
muito em intensidade. Por isto vamos querer que os raios
refletidos saiam paralelos. Assim evitamos a dispersão. O
sinal transmitido vai perder muito pouco em intensidade e
só vai poder ser captado em pontos que estiverem sobre a
semi-reta partido da fonte, com a direção escolhida.
A questão a ser considerada agora é a determinar a forma
que deve ter um espelho para que os raios emitidos por
uma fonte localizada um ponto
, e desejamos que este sinal seja captado
em um outro ponto, a grande distância. Fazemos com que
ele seja refletido por um anteparo. A fim de que o sinal
possa ser captado facilmente, não queremos que ele perca
muito em intensidade. Por isto vamos querer que os raios
refletidos saiam paralelos. Assim evitamos a dispersão. O
sinal transmitido vai perder muito pouco em intensidade e
só vai poder ser captado em pontos que estiverem sobre a
semi-reta partido da fonte, com a direção escolhida.
A questão a ser considerada agora é a determinar a forma
que deve ter um espelho para que os raios emitidos por
uma fonte localizada um ponto  sejam todos eles refletidos
paralelamente.
sejam todos eles refletidos
paralelamente.
O espelho é uma superfície
 , mas
cortando a superfície
, mas
cortando a superfície
 por um plano
que passa pelo ponto
por um plano
que passa pelo ponto  , obtemos uma curva
, obtemos uma curva
 .
Vamos considerar, então, o problema de determinar a forma
da curva
.
Vamos considerar, então, o problema de determinar a forma
da curva
 . Temos agora um problema em um
plano. Colocando neste plano um sistema de coordenadas
de modo que a origem fique sobre a fonte luminosa
. Temos agora um problema em um
plano. Colocando neste plano um sistema de coordenadas
de modo que a origem fique sobre a fonte luminosa  e
o eixo dos
e
o eixo dos  seja paralelo aos raios refletidos. Temos
que resolver um problema puramente geométrico,
representado na figura abaixo.
O problema que queremos resolver é o de determinar
as curvas
seja paralelo aos raios refletidos. Temos
que resolver um problema puramente geométrico,
representado na figura abaixo.
O problema que queremos resolver é o de determinar
as curvas
 com a propriedade descrita
a seguir. Dado um
ponto
com a propriedade descrita
a seguir. Dado um
ponto  qualquer sobre
qualquer sobre
 , seja
, seja  a reta
tangente à curva
a reta
tangente à curva
 no ponto
no ponto  .
Seja
.
Seja  o ângulo entre a tangente
o ângulo entre a tangente  e o
eixo
e o
eixo  (ou se, preferir, o raio refletido no ponto
(ou se, preferir, o raio refletido no ponto  )
e seja
)
e seja  o ângulo entre a reta
o ângulo entre a reta  e o raio
e o raio
 . Pela lei da reflexão, queremos
determinar as curvas
. Pela lei da reflexão, queremos
determinar as curvas
 que tenham a
propriedade que
que tenham a
propriedade que
 .
.
Vamos procurar a função  , cujo gráfico
é a curva
, cujo gráfico
é a curva
 . Seja
. Seja
 um ponto
genérico de
um ponto
genérico de
 . Temos
. Temos
 ,
pois são ângulos com lados paralelos
(um deles é até comum). Logo
,
pois são ângulos com lados paralelos
(um deles é até comum). Logo
 e o triângulo
e o triângulo  é isósceles. Logo
é isósceles. Logo
 . Mas
. Mas
 .
Pela interpretação
geométrica da derivada,
Logo
.
Pela interpretação
geométrica da derivada,
Logo
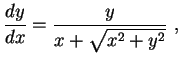 |
(1) |
que é uma equação diferencial satisfeita pela curva
 .
.
Resolução da equação diferencial (1):
Trata-se de uma equação diferencial homogênea. É
perfeitamente possível resolvê-la empregando os
métodos vistos em aula (faça como exercício).
No entanto, resulta um pouco mais simples transformá-a
na equação
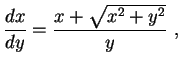 |
(2) |
que também é homogênea, pois pode ser reescrita como
com o lado direito dependendo somente da razão  .
Introduzindo a nova variável independente
obtemos a equação
isto é,
Separando as variáveis,
A segunda integral é calculada por uma substituição
trigonométrica
.
Introduzindo a nova variável independente
obtemos a equação
isto é,
Separando as variáveis,
A segunda integral é calculada por uma substituição
trigonométrica
 ,
,
 ,
Logo
,
Logo
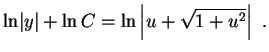
(

)
Logo
Multiplicando por  ,
Elevando ao quadrado,
ou seja,
Dividindo por
,
Elevando ao quadrado,
ou seja,
Dividindo por  ,
,
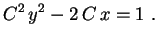 |
(3) |
Esta equação representa uma família de
parábolas (deitadas).
Interpretação da solução:
Uma maneira simples de localizar no plano a família
de parábolas dada pela equação (3) é completar o
quadrado, reescrevendo como,
isto é,
Dividindo por  , obtém-se
ou, extraindo a raiz quadrada,
, obtém-se
ou, extraindo a raiz quadrada,
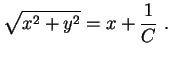 |
(4) |
O lado esquerdo da igualdade (4) representa a
distância do ponto
 à origem,
à origem,

|
enquanto que o lado direito
representa a distância do ponto  à reta vertical à reta vertical
 .
A igualdade (4) nos diz que cada curva da família .
A igualdade (4) nos diz que cada curva da família
 é caracterizada a partir de uma reta
diretriz é caracterizada a partir de uma reta
diretriz  , de equação , de equação  . Vale então a
propriedade que, para um ponto . Vale então a
propriedade que, para um ponto  qualquer sobre a curva qualquer sobre a curva
 , a distância , a distância
 de de  ao foco
ao foco  é igual à distância é igual à distância
 de
de  à reta diretriz à reta diretriz  . A cada valor escolhido
para a constante . A cada valor escolhido
para a constante  obtém-se uma parábola obtém-se uma parábola
 .
Fazendo variar .
Fazendo variar  , o foco
continua na origem e a reta diretriz se desloca.
Fazendo variar , o foco
continua na origem e a reta diretriz se desloca.
Fazendo variar  nos positivos, o plano menos
o semi-eixo positivo dos nos positivos, o plano menos
o semi-eixo positivo dos  se decompõe numa
família de parábolas. se decompõe numa
família de parábolas.
|
Se cortarmos a superfície
 por um outro
plano passando pelo foco
por um outro
plano passando pelo foco  , a seção resultante
seria também uma parábola membro da mesma
família, em princípio não necessariamente
a mesma parábola. Mas na verdade deve dar a mesma
parábola, pois caso contrário teríamos
uma descontinuidade na superfície
, a seção resultante
seria também uma parábola membro da mesma
família, em princípio não necessariamente
a mesma parábola. Mas na verdade deve dar a mesma
parábola, pois caso contrário teríamos
uma descontinuidade na superfície
 ,
já que diferentes parábolas da família
,
já que diferentes parábolas da família
 têm vértices distintos.
têm vértices distintos.
Conclusão:
Os únicos espelhos
com a propriedade que, quando sobre eles incide
um feixe de raios paralelos, os raios refletidos
concentram-se em um único ponto  , são
aqueles que têm a forma de um parabolóide
de revolução. Além disto, é preciso que
os raios incidentes sejam paralelos ao eixo do
parabolóide. O ponto
, são
aqueles que têm a forma de um parabolóide
de revolução. Além disto, é preciso que
os raios incidentes sejam paralelos ao eixo do
parabolóide. O ponto  vai se situar no
foco do parabolóide.
Em particular, epelhos esféricos têm sempre
uma aberração, os raios refletidos não se
concentram exatemente em um único ponto.
vai se situar no
foco do parabolóide.
Em particular, epelhos esféricos têm sempre
uma aberração, os raios refletidos não se
concentram exatemente em um único ponto.


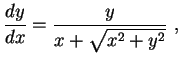
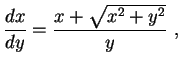






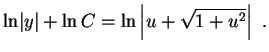 (
(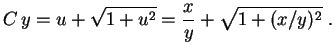

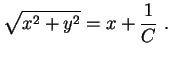

 .
A igualdade (4) nos diz que cada curva da família
.
A igualdade (4) nos diz que cada curva da família
![]() , são
aqueles que têm a forma de um parabolóide
de revolução. Além disto, é preciso que
os raios incidentes sejam paralelos ao eixo do
parabolóide. O ponto
, são
aqueles que têm a forma de um parabolóide
de revolução. Além disto, é preciso que
os raios incidentes sejam paralelos ao eixo do
parabolóide. O ponto ![]() vai se situar no
foco do parabolóide.
Em particular, epelhos esféricos têm sempre
uma aberração, os raios refletidos não se
concentram exatemente em um único ponto.
vai se situar no
foco do parabolóide.
Em particular, epelhos esféricos têm sempre
uma aberração, os raios refletidos não se
concentram exatemente em um único ponto.