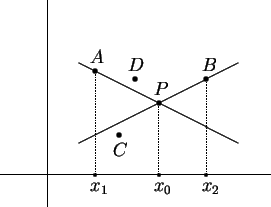
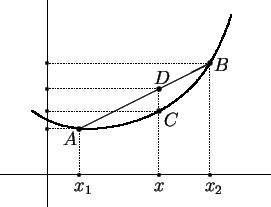
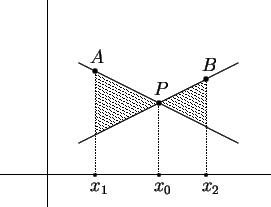
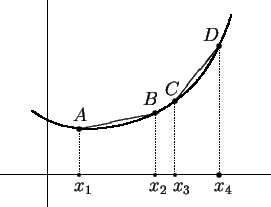
então existiria um ponto
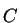 ou um
ponto ou um
ponto 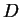 como na figura ao lado, ou ainda pontos
análogos, à direita de como na figura ao lado, ou ainda pontos
análogos, à direita de 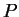 . Mas qualquer uma destas
possibilidades iria contrariar o fato de . Mas qualquer uma destas
possibilidades iria contrariar o fato de 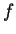 ser convexa.
Por exemplo, um ponto como ser convexa.
Por exemplo, um ponto como 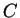 não pode pertencer ao
gráfico de não pode pertencer ao
gráfico de
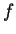 , pois, se pertencesse, o ponto , pois, se pertencesse, o ponto 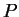 estaria acima
do segmento estaria acima
do segmento
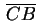 . Um ponto como . Um ponto como 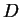 não pode pertencer ao gráfico de
não pode pertencer ao gráfico de 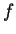 , pois, se
pertencesse, o ponto , pois, se
pertencesse, o ponto 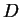 estaria acima do segmento estaria acima do segmento
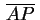 . Fica assim estabelecido que o
gráfico de . Fica assim estabelecido que o
gráfico de 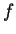 fica contido na região fica contido na região
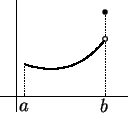
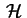 . Daí segue que . Daí segue que 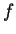 é
contínua no ponto é
contínua no ponto 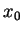 , pois deve satisfazer
uma desigualdade da forma , pois deve satisfazer
uma desigualdade da forma
|
|
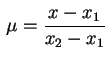 , temos
, temos

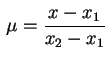 , temos
, temos
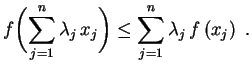
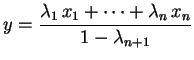
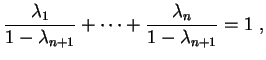
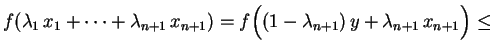
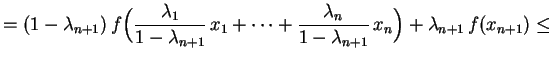
![$\displaystyle \leq(1-\lambda_{n+1})\biggl[
\frac{\lambda_1}{1-\lambda_{n+1}}\,...
...\frac{\lambda_n}{1-\lambda_{n+1}}\,f(x_n)\biggr]
+\lambda_{n+1}\,f(x_{n+1})=
$](img49.gif)

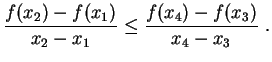
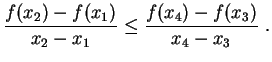
![$\displaystyle \hspace{1.9cm}
=\lambda\Bigl[f(x_1)-f(\lambda\,x_1+\mu\,x_2)\Bigr]+
\mu\Bigl[f(x_2)-f(\lambda\,x_1+\mu\,x_2)\Bigr] \ .
$](img104.gif)
![$\displaystyle L=\lambda\,\mu\bigl(x_2-x_1\bigr)\Bigl[-f'(y_1)+
f'(y_2)\Bigr]\geq 0 \ .
$](img110.gif)
![$\displaystyle \sqrt[n]{a_1\,a_2\ldots a_n}\leq
\frac{a_1+a_2+\cdots+a_n}{n} \ \ ,
$](img122.gif)
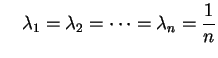
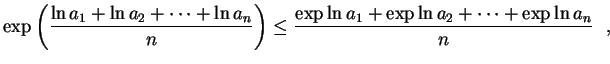
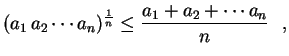
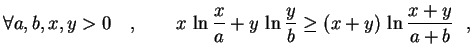
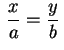 .
.
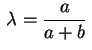 e
e
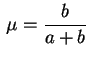 , temos
, temos
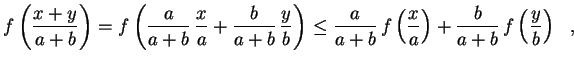
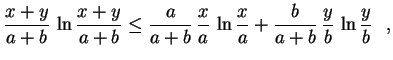
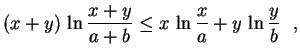
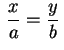 .
.
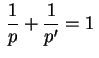 . Mostre que
para todos a, b>0
. Mostre que
para todos a, b>0
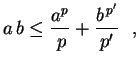
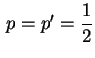 . Temos, então, a
desigualdade bem conhecida
. Temos, então, a
desigualdade bem conhecida
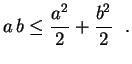
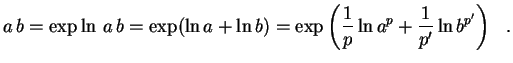
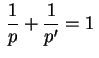 ,
usando o fato que a função exponencial é
estritamente convexa, temos,
,
usando o fato que a função exponencial é
estritamente convexa, temos,
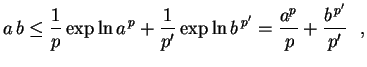
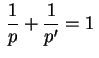 e
e
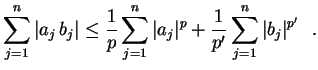
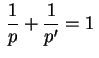 .
Para quaisquer vetores
.
Para quaisquer vetores
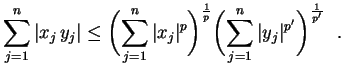
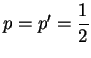 ,
é a Desigualdade de Cauchy-Schwarz.
,
é a Desigualdade de Cauchy-Schwarz.
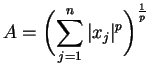 e
e 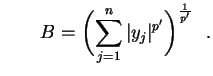
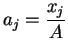 e
e
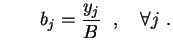
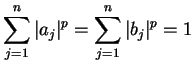
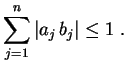
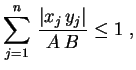
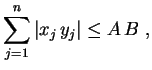
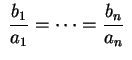 .
.
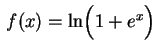 . Temos
. Temos
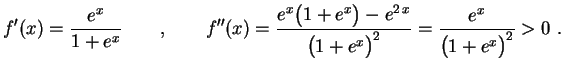
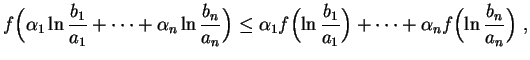
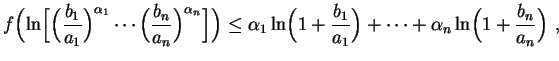
![$\displaystyle \ln\biggl(1+\frac{b_1^{\alpha_1}\cdots b_n^{\alpha_n}}
{a_1^{\al...
...gr)^{\alpha_1}
\cdots\Bigl(\frac{a_n+b_n}{a_n}\Bigr)^{\alpha_n}
\biggr] \ .
$](img193.gif)
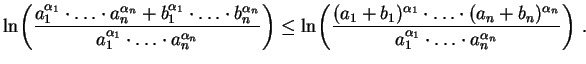
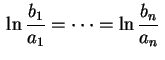 , isto é, se e somente se
, isto é, se e somente se
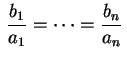 .
.