CAMPO ELÉTRICO GERADO POR DOIS FIOS PARALELOS



O objetivo deste texto é o de apresentar uma aplicação interessante de trajetórias ortogonais Consideremos o problema de determinar as linhas de campo e as superfícies equipotenciais do campo elétrico gerado por dois fios paralelos de material condutor, carregados com cargas opostas de mesma densidade. Devido à simetria do problema, só duas dimensões de espaço são relevantes. Tomando um sistema de coordenadas em que o eixo $ Z$ seja paralelo aos fios, o campo, o potencial e as forças elétricas vão depender só das coordenadas $ x$ e $ y$. Podemos visualizar o problema no plano. Mas na verdade um ponto deste plano vai representar uma reta no espaço tridimensional (a reta passando pelo ponto e paralela ao eixo $ Z$). É como se estivéssemos olhando de cima e víssemos a reta como um ponto,

     \begin{picture}(150,135) \put(10,60){\line(1,0){130}} \put(70,10){\line(0,1){1... ...6,5){56}} \put(103.5,106){\circle*{3}} \put(105,108){\mbox{$P$}} \end{picture}           
um cilindro como um círculo, e assim por diante. Na Figura 1, os pontos $ A$ e $ B$ representam fios paralelos de um material condutor. Sejam $ \lambda$ ($ \lambda>0$) a densidade linear de carga (carga por unidade de comprimento) do fio $ A$ e $ -\lambda$ a densidade de carga do fio $ B$. Estamos interessados no campo elétrico num ponto $ P$. Queremos encontrar a linha de campo e a superfície equipotencial passando por $ P$. Vamos primeiro encontrar o potencial gerado por um único fio e depois, somando os resultados, obter o potencial gerado pelos dois fios.


Potencial gerado por um fio. A origem representa agora um fio de material condutor, a densidade de carga vale $ \,\lambda\,$ e queremos saber o valor do potencial elétrico no ponto $ P$.

       \begin{picture}(120,120) \put(20,5){\line(0,1){110}} \put(20,60){\circle*{3}} ... ...1){5}} \put(19.5,18){\line(0,1){5}} \put(20.5,18){\line(0,1){5}} \end{picture}             
Por uma questão de simetria, o campo elétrico $ \vec{E}$ vai ser perpendicular ao fio e sua intensidade não vai depender da coordenada $ Z$. Dado um ponto $ P$ no espaço, seja $ O$ o ponto do fio mais próximo de $ P$. Coloquemos sobre o fio a coordenada 0 no ponto $ O$. Sejam $ d\vec{E_1}$ e $ d\vec{E_2}$ os campos elétricos gerados por segmentos de comprimento $ dz$ medidos, repectivamente, a partir dos pontos de coordenada $ z$ e $ -z$. A carga elétrica em cada um destes segmentos vale $ \lambda\,dz$. Seja $ d\vec{E}$ a resultante de $ d\vec{E_1}$ e $ d\vec{E_2}$.
A componente vertical de $ d\vec{E}$ é nula e a componente horizontal vale

$\displaystyle dE=\lvert d\vec{E}\rvert=2\,\lvert\vec{dE_1}\rvert\cdot \cos\alph... ...ambda\,\rho}{2\,\pi\,\epsilon_0}\frac{dz} {\bigl(\rho^2+z^2\bigr)^\frac32}\ .$

Logo a intensidade no ponto $ P$ do campo gerado pela carga distribuída ao longo de todo o fio vale

$\displaystyle E=\frac{\lambda\,\rho}{2\,\pi\,\epsilon_0}\int_0^\infty \frac{dz}... ...1+\left(\frac{z}{\rho}\right)^2 \Bigr)^\frac32}\,d\left(\frac{z}{\rho}\right)$

e, fazendo uma mudança de variável $ \,w=z/\rho\,$,

$\displaystyle E=\frac{\lambda}{2\,\pi\,\epsilon_0\,\rho}\left. \Biggl(-\Bigl[1+... ...\Biggr)\right\vert _{z=0}^{z=\infty} =\frac{\lambda}{2\,\pi\,\epsilon_0\,\rho}$ (1)

Para obter o potencial elétrico $ u$, lembremos que

$\displaystyle \vec{E}=-\nabla u \ .$

Mas a função $ u$ depende apenas da distância $ \rho$ do ponto $ P$ ao eixo $ Z$. Isto é, é da forma $ u=u(\rho)$. Portanto

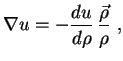
$\displaystyle \nabla u=-\frac{du}{d\rho}\,\frac{\vec{\rho}}{\rho} \ , $

onde $ \vec{\rho}=(x,y,0)$ e $ \rho=\lvert\rho\rvert=\sqrt{x^2+y^2}\,$. Comparando com

$\displaystyle \vec{E}=\frac{\lambda}{2\,\pi\,\epsilon_0\,\rho}\,\frac{\vec{\rho}}{\rho} \ ,$

que decorre da expressão (1) obtida acima, vemos que deve-se ter

$\displaystyle \frac{du}{d\rho} =-\frac{\lambda}{2\,\pi\,\epsilon_0\,\rho} \ .$

Portanto $ u$ é do tipo

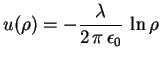$\displaystyle u(\rho)=-\frac{\lambda} {2\,\pi\,\epsilon_0}\,\ln \rho+C \ ,$

para alguma constante $ C$. Qual o valor da constante? Lembremos que o importante é não tanto o potencial em cada ponto, mas sim a diferença de potencial entre pares de pontos (por exemplo, o trabalho realizado pela força elétrica sobre uma carga que se desloca entre dois pontos vale o produto da carga pela diferença de potencial entre os dois pontos). Portanto o valor da constante $ C$ não é relevante, pois $ C$ é cancelada quando se calcula a diferença de potencial. Fazemos então a escolha mais simples possível, $ \,C=0\,$. Chegamos assim à expressão

$\displaystyle u(\rho)=-\frac{\lambda}{2\,\pi\,\epsilon_0}\,\ln \rho$ (2)

para o potencial gerado por uma distribuição uniforme de carga elétrica sobre um fio infinitamente longo, sendo $ \lambda$ a densidade linear de carga.

Potencial gerado pelos dois fios. Para fixar as idéias, suponhamos que, na Figura 1, os pontos $ A$ e $ B$ tenham coordenadas $ \,A=(1,0)\,$ e $ \,B=(-1,0)\,$. As distâncias $ \,d_A=\lvert AP\rvert\,$ e $ \,d_B=\lvert BP\rvert\,$ valem, então,

$\displaystyle d_A=\sqrt{(x-1)^2+y^2}$    e $\displaystyle \qquad d_B=\sqrt{(x+1)^2+y^2} \ .$

O potencial $ u$ gerado pelos dois fios, sendo a soma dos potenciais gerados por cada um dos fios individualmente, vale

$\displaystyle u=-\frac{\lambda}{2\,\pi\,\epsilon_0}\bigl(\ln d_A-\ln d_B\bigr)=... ...{\lambda}{2\,\pi\,\epsilon_0}\ln\biggl( \frac{(x+1)^2+y^2}{(x-1)^2+y^2}\biggr) $

Logo as superfícies equipotenciais (representadas por curvas no plano $ XY$) são a família das curvas de nível

$\displaystyle \ln\biggl(\frac{(x+1)^2+y^2}{(x-1)^2+y^2}\biggr)=K \ , \qquad (\,-\infty<K<+\infty\,)$

ou, equivalentemente (escrevendo $ \,K=\ln C\,$),

$\displaystyle \frac{(x+1)^2+y^2}{(x-1)^2+y^2}=C \ , \qquad (\,C>0\,) \ .$ (3)

Reescrevemos (3) como

$\displaystyle (x+1)^2+y^2=C\,\bigl((x-1)^2+y^2\bigr) \ ,$

isto é,

$\displaystyle \bigl(C-1\bigr)\bigl(x^2+y^2+1\bigr)=2\bigl(C+1\bigr)x \ .$ (4)

Para $ \,C\neq 1\,$, (4) representa uma família de círculos. Porém, um membro desta família, para $ \,C=1\,$, é o eixo $ \,Y\,$, $ \,x=0\,$. Chamando de $ \displaystyle\,D=\frac{C+1}{C-1}\,\rule{0.cm}{0.7cm}$, podemos reescrever (4) na forma

$\displaystyle x^2+y^2+1=2\,D\,x \ .$ (5)

A maneira mais simples de descobrir a variação do parâmetro $ D$ é olhando para o gráfico

      \begin{picture}(200,150) \put(10,70){\line(1,0){180}} \put(90,10){\line(0,1){1... ... \qbezier(20,87)(83,85)(104,20) \qbezier(115,135)(120,95)(180,93) \end{picture}           
da função $ \,D=f(C)=\displaystyle\,D=\frac{C+1}{C-1}\,\rule{0.cm}{0.7cm}$. Vemos que quando $ \,C\,\rule{0.cm}{0.4cm}$ varia no intervalo $ \,0<C<\infty\,$, vamos ter que $ \,D\,$ varia no conjunto $ \,\lvert D\rvert>1\,$, ou seja

$\displaystyle \,D\in(-\infty,-1)\cup(1,\infty) \ .$

Completando o quadrado na expressão (5), tem-se

$\displaystyle x^2-2\,D\,x+D^2+y^2=D^2-1 \ ,$

isto é,

$\displaystyle (x-D)^2+y^2=D^2-1 \ . $
A conclusão é que as superfícies equipotenciais são os círculos (na realidade, cilindros circulares) centrados em pontos $ \,(D,0)\,$ de raio $ \,\sqrt{D^2-1}\,$, para $ \,\lvert D\rvert>1\,$.

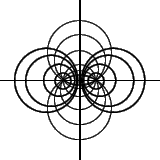
Linhas de campo. Para determinar as linhas de campo do campo elétrico gerado pelos dois fios, usamos o fato que as linhas de campo e as superfícies equipotenciais cortam-se sempre ortogonalmente. Portanto, do ponto de vista matemático, o problema que queremos resolver é o de determinar as trajetórias ortogonais à família de círculos (5).

Solução do problema. Seja $ \,\mathcal{F}_1\,$ a família de círculos (5) e seja $ \,\mathcal{F}_2\,$ a família das trajetórias ortogonais à família $ \,\mathcal{F}_1\,$. O primeiro passo é encontrar uma equação diferencial de primeira ordem, da qual $ \,\mathcal{F}_1\,$ seja a solução geral. Reescrevendo (5) como

$\displaystyle \frac{x^2+y^2+1}{x}=2\,D \ , $

pensando em $ y$ como função de $ x$ e derivando em relação a $ x$, obtém-se

$\displaystyle \frac{(2\,x+2\,y\,y')\,x-(x^2+y^2+1)}{x^2}=0 \ . $

O numerador desta fração deve se anular. Logo

$\displaystyle 2\,x\,y\,y'+x^2-y^2-1=0 \ . $

Logo os círculos da família $ \,\mathcal{F}_1\,$ dada satisfazem, todos eles, a equação diferencial em forma normal

$\displaystyle y'=\frac{y^2-x^2+1}{2\,x\,y} \ . $

Usando a condição de ortogonalidade, a família ortogonal $ \,\mathcal{F}_2\,$ deve satisfazer

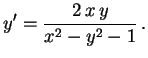
$\displaystyle y'=\frac{2\,x\,y}{x^2-y^2-1} \, .$ (6)

Para resolver (6), reescrevemos esta equação como

$\displaystyle 2\,x\,y\,dx+(y^2-x^2+1)\,dy=0 \ .$ (7)

Vamos procurar um fator integrante para (7). Investigando a existência de um fator integrante $ \,\mu(y)\,$ dependendo só de $ y\,$, multiplicamos (7) por $ \,\mu(y)\,$, obtendo

$\displaystyle 2\,x\,y\,\mu(y)\,dx+(y^2-x^2+1)\,\mu(y)\,dy=0 \ . $

A condição para que esta última seja uma equação exata é que

$\displaystyle \Bigl(2\,x\,y\,\mu(y) \Bigr)_y= \Bigl(y^2-x^2+1)\,\mu(y)\Bigr)_x \ , $

isto é,

$\displaystyle 2\,x\bigl(\mu(y)+y\,\mu'(y)\bigr)=-2\,x\,\mu(y) $

ou ainda,

$\displaystyle \mu(y)+y\,\mu'(y)=-\mu(y) \ .$ (8)

Como $ x$ foi eliminado, a condição (8) é uma equação diferencial ordinária, que pode ser facilmente resolvida separando as variáveis,

$\displaystyle y\,\frac{d\mu}{dy}=-2\,\mu \quad , \quad \int\frac{d\mu}{\mu}=\int-2\, \frac{dy}{y} \ .$

Não estamos interessados na solução geral desta última equação diferencial. Basta-nos ter um fator integrante. Escolhendo, então, a constante de integração como 0, obtemos

$\displaystyle \ln\mu=-2\,\ln y \ .$

Encontramos assim o fator integrante $ \,\mu=y^{-2}\,$ para (7). Multiplicando (7) por $ \,\mu=y^{-2}\,$, obtém-se a equação exata

$\displaystyle 2\,x\,y^{-1}\,dx+(1-x^2y^{-2}+y^{-2})\,dy=0 \ .$

Para resolvê-la, queremos encontrar uma função de duas variáveis $ \,F(x,y)\,$ satisfazendo

$\displaystyle \left\{\begin{array}{l} \displaystyle\frac{\partial F}{\partial ... ...artial F}{\partial y}=1-x^2y^{-2}+y^{-2} \rule{0.cm}{0.9cm}\end{array}\right.$ (9)

Da primeira condição acima segue que

$\displaystyle F(x,y)=x^2\,y^{-1}+\varphi(y) \, ,$ (10)

com $ \,\varphi(y)\,$ dependendo só de $ \,y\,$. Derivando (10) em relação a $ \,y\,$,

$\displaystyle \frac{\partial F}{\partial y}=-x^2y^{-2}+\varphi'(y)$

e comparando esta última com a segunda condição em (9), segue que

$\displaystyle \varphi'(y)=1+y^{-2} \ .$

Integrando esta última e tomando a constante de integração como sendo 0, segue

$\displaystyle \varphi(y)=y-y^{-1} \ .$

Portanto uma função que satisfaz (9) é

$\displaystyle F(x,y)=x^2\,y^{-1}+y-y^{-1} \ .$

Logo a solução geral de (7) é

$\displaystyle x^2\,y^{-1}+y-y^{-1}=C \ ,$

que pode ser reescrita de maneira mais simples como

$\displaystyle x^2+y^2-C\,y-1=0 \, .$ (11)

Logo a família $ \,\mathcal{F}_2\,$ das linhas de campo também é uma família de círculos. É imediato

\begin{picture}(80,90) \put(0,50){\line(1,0){100}} \put(50,67.5){\circle{40}} ... ...rcle{30}} \put(28.9,50){\circle{40}} \put(50,0){\line(0,1){100}} \end{picture}         
verificar que $ \,x=\pm 1\,$, $ \,y=0\,$ são soluções de (11). Logo a família $ \mathcal{F}_2$ das linhas campo é a família dos círculos que passam pelos pontos $ \,(1,0)\,$ e $ \,(-1,0)\,$. A figura ao lado representa as duas famílias de círculos. Os círculos traçados com linhas mais grossas representam a família $ \,\mathcal{F}_1\,$ das linhas equipotenciais e os círculos desenhados com linhas mais finas representam a família $ \,\mathcal{F}_2\,$ das linhas de campo.


Eduardo H. M. Brietzke