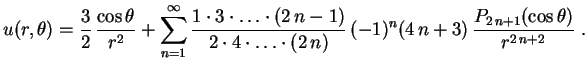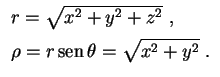
Laplaciano em Coordenadas Esféricas



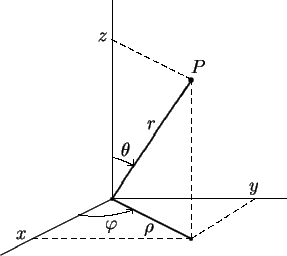
Vamos usar os símbolos $ (r,\theta,\varphi)$ para indicar as coordenadas esféricas de um ponto.

\begin{picture}(190,177) \put(75,40){\line(0,1){125}} \put(75,40){\line(1,0){1... ...klines \put(75,40){\line(2,-1){50}} \put(75,40){\line(2,3){50}} \end{picture}          
Temos

$\displaystyle \begin{array}{l} x=r\,\,{\rm sen}\,\theta\,\cos\varphi \ , \\ y=... ...hi \ ,\rule{0.cm}{0.4cm} \\ z=r\,\cos\theta \ ,\rule{0.cm}{0.4cm} \end{array} $

e também

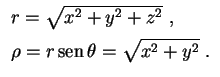
$\displaystyle \begin{array}{l} r=\sqrt{x^2+y^2+z^2} \ , \\ \rho=r\,{\rm sen}\,\theta=\sqrt{x^2+y^2} \ .\rule{0.cm}{0.6cm} \end{array} $

Nosso objetivo é expressar o laplaciano em 3 variáveis

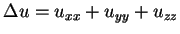
$\displaystyle \Delta u=u_{xx}+u_{yy}+u_{zz} $



em termos das coordenadas esféricas $ (r,\theta,\varphi)$. Um cálculo direto é bastante longo. Por isto seguimos outro caminho. Usando a expressão do laplaciano em 2 variáveis em termos das coordenadas polares, temos

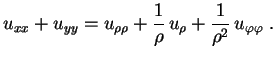$\displaystyle u_{xx}+u_{yy}=u_{\rho\rho}+\frac{1}{\rho}\,u_\rho+ \frac{1}{\rho^2}\,u_{\varphi\varphi} \ .$ (1)

Notemos que as relações

$\displaystyle z=r\,\cos\theta \qquad , \qquad \rho=r\,\,{\rm sen}\,\theta $

são análogas às relações entre as coordenadas cartesianas e polares no plano, somente, agora, com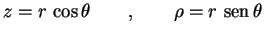 $ z$ e $ \rho$ desempenhando, respectivamente, os papéis de $ x$ e $ y$. Portanto, usando novamente a expressão do laplaciano em cordenadas polares, podemos escrever

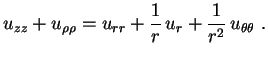$\displaystyle u_{zz}+u_{\rho\rho}= u_{rr}+\frac{1}{r}\,u_r+\frac{1}{r^2}\,u_{\theta\theta} \ .$ (2)

Somando $ u_{zz}$ a ambos os lados em (1) temos

$\displaystyle \Delta u= u_{xx}+u_{yy}+u_{zz}=u_{\rho\rho}+u_{zz} +\frac{1}{\rho}\,u_\rho+\frac{1}{\rho^2}\,u_{\varphi\varphi} $

e, usando (2),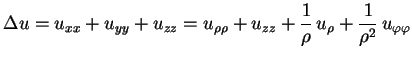

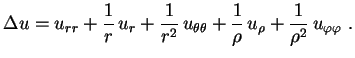$\displaystyle \Delta u= u_{rr}+\frac{1}{r}\,u_r+\frac{1}{r^2}\,u_{\theta\theta}+ \frac{1}{\rho}\,u_\rho+\frac{1}{\rho^2}\,u_{\varphi\varphi} \ .$ (3)

Precisamos expressar $ u_\rho$ em coordenadas esféricas. Pela regra da cadeia

$\displaystyle u_\rho=u_r\,r_\rho+u_\theta\,\theta_\rho+ u_\varphi\,\varphi_\rho \ . $

Em (1), estávamos mantendo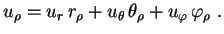 $ z$ fixo e tomando $ \rho$ e $ \varphi$ como variáveis independentes, de modo que $ \,\varphi_\rho=0\,$. Portanto

$\displaystyl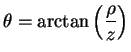e u_\rho=u_r\,r_\rho+u_\theta\,\theta_\rho \ .$ (4)

De

$\displaystyle \theta=\arctan\left(\frac{\rho}{z}\right) $

segue que

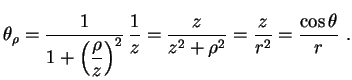$\displaystyle \theta_\rho=\frac{1}{1+\left(\displaystyle \frac{\rho}{z}\right)^2}\,\frac{1}{z}= \frac{z}{z^2+\rho^2}=\frac{z}{r^2}= \frac{\cos\theta}{r} \ .$ (5)

Por outro lado, de

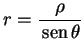$\displaystyle r=\frac{\rho}{\,{\rm sen}\,\theta}$ (6)

segue que

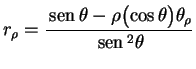$\displaystyle r_\rho=\frac{\,{\rm sen}\,\theta-\rho\bigl(\cos\theta\bigr)\theta_\rho} {\,{\rm sen}\,^2\theta}$ (7)

Usando (5) e (6) em (7), obtém-se

$\displaystyle r_\rho=\,{\rm sen}\,\theta \ .$ (8)

Finalmente, substituindo (5) e (6) em (4), segue que

$\displaystyle u_\rho=\bigl(\,{\rm sen}\,\theta\bigr)u_r+ \frac{\cos\theta}{r}\,u_\theta $

e, portanto,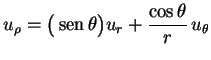

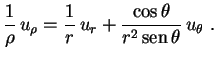$\displaystyle \frac{1}{\rho}\,u_\rho=\frac{1}{r}\,u_r+ \frac{\cos\theta}{r^2\,{\rm sen}\,\theta}\,u_\theta \ .$ (9)

Finalmene, substituindo (9) em (3), obtemos

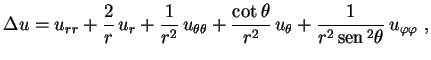$\displaystyle \Delta u=u_{rr}+\frac{2}{r}\,u_r+\frac{1}{r^2}\,u_{\theta\theta}+... ...eta}{r^2}\,u_\theta+ \frac{1}{r^2\,{\rm sen}\,^2\theta}\,u_{\varphi\varphi} \ ,$ (10)

que é a expressão do laplaciano em coordenadas esféricas.

Simetria Axial

Vamos considerar somente problemas com simetria axial, isto é, o caso em que a função $ \,u\,$ independe de $ \,\varphi\,$, dependendo apenas de $ \,r\,$ e $ \,\theta\,$. As derivadas em relação a $ \,\varphi\,$ se anulam e a expressão do laplaciano então se simplifica um pouco,

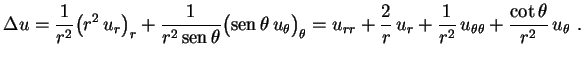$\displaystyle \Delta u=\frac{1}{r^2}\bigl(r^2\,u_r\bigr)_r+ \frac{1}{r^2\,\text... ...}{r}\,u_r+\frac{1}{r^2}\,u_{ \theta\theta}+\frac{\cot\theta}{r^2}\,u_\theta \ .$ (11)


Exemplo Dois hemisférios condutores de raio 1 são carregados até atingirem os potenciais de $ +1\,$ e $ \,-1\,\rule{0.cm}{0.4cm}$, respectivamente.

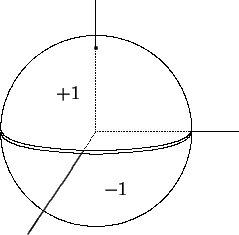
  \begin{picture}(150,150) \put(70,112) {\line (0,1){30}} \qbezier(130,61)(130,7... ...(-2,-3){34.5}} \put(45,80){\mbox{$+1$}} \put(75,20){\mbox{$-1$}} \end{picture}         
Determinar o potencial:

(a) Na região interior;

(b) Na região exterior.

                  Solução:

(a) Na região interior

$\displaystyle \left\{ \begin{array}{l} \Delta u=0 \ , \quad\mbox{para } \ r<1 \... ...{\pi}{2}<\theta<\pi \rule{0.cm}{0.5cm} \end{array} \right. \end{array} \right. $

Como o potencial na esfera independe de $ \varphi\,\rule{0.cm}{0.6cm}$, no $ \,\mathbb{R}^3\,$ todo também vai independer, isto é, a solução $ \,u\,$ vai depender apenas de $ r$ e $ \theta$. Temos, portanto, para $ u=u(r,\theta)\,$, o problema de Dirichlet

$\displaystyle \left\{ \begin{array}{l} \displaystyle u_{rr}+\frac{2}{r}\,u_r+\f... ...{\pi}{2}<\theta<\pi \rule{0.cm}{0.5cm} \end{array} \right. \end{array} \right. $

Resolvendo por separação de variáveis, iniciamos substituindo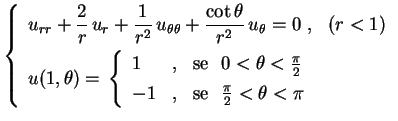 $ \,u(r,\theta)=F(r)\,G(\theta)\,$ na equação diferencial. Obtemos

$\displaystyle F''(r)\,G(\theta)+\frac{2}{r}\,F'(r)\,G(\theta)+ \frac{1}{r^2}\,F(r)\,G''(\theta)+ \frac{\cot\theta}{r^2}\,F(r)\,G'(\theta)=0 \ . $

Multiplicando por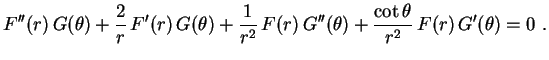 $ \,r^2\,$ e dividindo por $ \,F(r)\,G(\theta)\,$, separamos as variáveis

$\displaystyle \frac{r^2\,F''(r)+2\,r\,F'(r)}{F(r)}=- \frac{G''(\theta)+(\cot\theta)\,G'(\theta)}{G(\theta)}= \lambda \ . $

Seguem daí as duas equações diferenciais independentes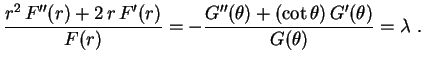

$\displaystyle r^2\,F''(r)+2\,r\,F'(r)-\lambda\,F(r)=0$    e $\displaystyle \qquad G''(\theta)+(\cot\theta)\,G'(\theta)+\lambda\,G(\theta)=0 \ . $

Apesar de mais complicada, vamos começar resolvendo a segunda equação.

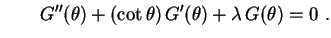
Este é um problema clássico, para o qual existe um método também clássico de resolução. Ele consiste em fazer a mudança de variável $ \,\mu=\cos\theta\,$.

$\displaystyle \begin{array}{l} \displaystyle G'(\theta)=\frac{dG}{d\theta}=\fra... ...d\mu}+\text{sen}^2\,\theta\,\frac{d^2G}{d\mu^2} \rule{0.cm}{0.8cm} \end{array} $

Substituindo na equação diferencial obtemos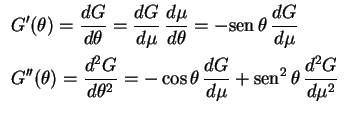

$\displaystyle \bigl(1-\cos^2\theta\bigr)\,\frac{d^2G}{d\mu^2}- 2\,\mu\,\frac{dG}{d\mu}+\lambda\,G=0 \ , $

isto é,

$\displaystyle \bigl(1-\mu^2\bigr)\,\frac{d^2G}{d\mu^2}- 2\,\mu\,\frac{dG}{d\mu}+\lambda\,G=0 \ , $

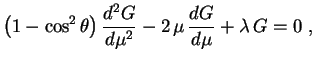que é a já estudada equação de Legendre. Como a variação de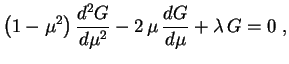 $ \theta\,$ é no intervalo $ \,0\leq\theta\leq\pi\,$, segue que $ \,\mu=\cos\theta\,$ varia no intervalo $ -1\leq\mu\leq 1\,$. Mas só nos servem soluções limitadas da equação de Legendre no intervalo $ \,[-1,1]\,$, soluções que sejam definidas e finitas para $ \,\mu=\pm1\,$. Como vimos acima, isto só acontece para

$\displaystyle \lambda_n=n\,(n+1)\qquad , \qquad G_n=P_n(\mu)= P_n(\cos\theta)\, \ . $

Substituindo este valor de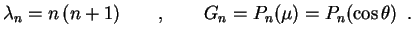 $ \,\lambda\,$ na outra equação, obtemos a equação de Euler-Cauchy

$\displaystyle r^2\,F''(r)+2\,r\,F'(r)-n\,(n+1)\,F(r)=0 \ , $

cuja solução geral é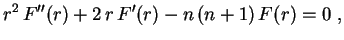

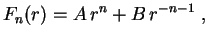
$\displaystyle F_n(r)=A\,r^n+B\,r^{-n-1} \ , $

pois $ \,m_1=n\,$ e $ \,m_2=-n-1\,$ são as soluções da equação $ \,m\,(m-1)+2\,m-n\,(n+1)=0 \,$.

Os cálculos que fizemos até aqui são válidos tanto para a região interior quanto exterior à esfera. Seriam válidos também para a região entre duas esferas centradas na origem.

Conclusão: Procurando pelo método de separação de variáveis, as funções da forma

$\displaystyle u(r,\theta)=F(r)\,G(\theta) $

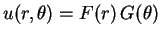
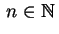
satisfazendo a equação de Laplace $ \,\Delta u=0\,$, encontramos para cada $ \,n\in\mathbb{N}\,$

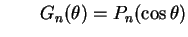
$\displaystyle F_n(r)=A\,r^n+B\,r^{-n-1}$    e $\displaystyle \qquad G_n(\theta)=P_n(\cos\theta) $



Neste ponto vamos começar a tratar especificamente o problema de Dirichlet para a região interior à esfera. Estamos procurando soluções definidas inclusive na origem, onde $ \,r=0\,$. Logo $ \,B=0\,$, pois $ \,r^{-n-1}$ se torna infinita na origem. Assim,

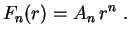$\displaystyle F_n(r)=A_n\,r^n \ . $

e, então,

$\displaystyle u_n(r,\theta)=A_n\,r^nP_n(\cos\theta) \ . $

Fazendo a superposição, temos

$\displaystyle u(r,\theta)=\sum_{n=0}^\infty\,A_n\,r^nP_n(\cos\theta) \ . $

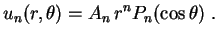As condições de fronteira

$\displaystyle u(1,\theta)=\sum_{n=0}^\infty\,A_n\,P_n(\cos\theta)= \rule{0.cm}{... ...& \mbox{se } \ \frac{\pi}{2}<\theta<\pi \rule{0.cm}{0.5cm} \end{array} \right. $

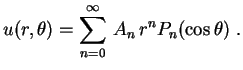nos dizem que os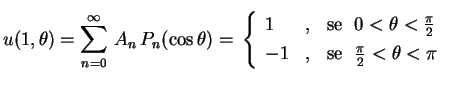 $ A_n$ são os coeficientes da expansão

$\displaystyle \sum_{n=0}^\infty\,A_n\,P_n(\cos\theta)=F(\mu)= \left\{ \begin{ar... ...mu<1 \\ -1 & , & \mbox{se } \ -1<\mu<0 \rule{0.cm}{0.5cm} \end{array} \right. $

Sabemos que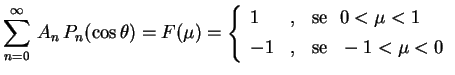

$\displaystyle A_n=\frac{2\,n+1}{2}\int_{-1}^{\,1}\,F(\mu)\, P_n(\mu)\,d\mu \ . $

A integral acima foi calculada em um exercício da lista,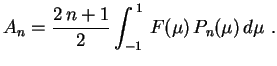

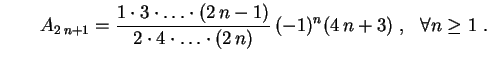$\displaystyle A_{2\,n}=0$    e $\displaystyle \qquad A_{2\,n+1}=\frac{1\cdot3\cdot\ldots\cdot(2\,n-1)} {2\cdot4\cdot\ldots\cdot(2\,n)}\,(-1)^n(4\,n+3) \ , \ \ \forall n\geq 1 \ . $

$\displaystyle A_1=\frac32\int_{-1}^{\,1}\,F(\mu)\, P_1(\mu)\,d\mu=3\int_0^1\mu\,d\mu=\frac32 $

Logo, na região interior à esfera,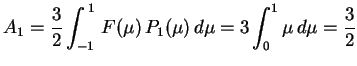 $ \,r<1\,$,

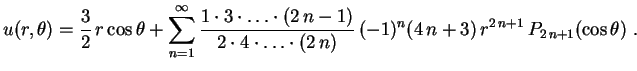
$\displaystyle u(r,\theta)=\frac32\,r\cos\theta+\sum_{n=1}^\infty \frac{1\cdot3\... ...dot\ldots\cdot(2\,n)}\,(-1)^n(4\,n+3)\, r^{2\,n+1}\,P_{2\,n+1}(\cos\theta) \ . $



(b) Na região exterior

Passamos agora a considerar o problema de Dirichlet

$\displaystyle \left\{ \begin{array}{l} \displaystyle u_{rr}+\frac{2}{r}\,u_r+\f... ...lim_{r\rightarrow\infty}\,u(r,\theta)=0 \rule{0.cm}{0.7cm} \end{array} \right. $

A solução é igual ao anterior, exceto que agora, para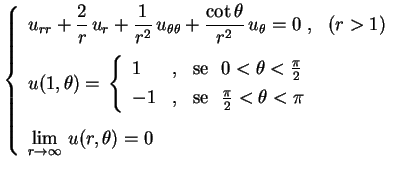

$\displaystyle F(r)=A\,r^n+\frac{B}{r^{n+1}} $

a condição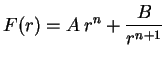 $ \,\displaystyle\lim_ {r\rightarrow\infty}\,F(r)=0\,$ nos dá $ \,A=0\,$, isto é,

$\displaystyle F(r)=\frac{B}{r^{n+1}} \ . $

A solução, então é,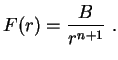

$\displaystyle u(r,\theta)=\sum_{n=0}^\infty\,\frac{B_n}{r^{n+1}}\, P_n(\cos\theta) \ . $

Como acima, obtemos

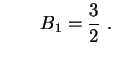
$\displaystyle B_{2\,n}=0 \quad , \qquad B_{2\,n+1}=\frac{1\cdot3\cdot\ldots\cdot(2\,n-1)} {2\cdot4\cdot\ldots\cdot(2\,n)}\,(-1)^n(4\,n+3) \ , \ \ \forall n\geq 1$    e $\displaystyle \qquad B_1=\frac32 \ . $

Logo, na região exterior à esfera, $ \,r>1\,$,

$\displaystyle u(r,\theta)=\frac32\,\frac{\cos\theta}{r^2}+ \sum_{n=1}^\infty \f... ...ts\cdot(2\,n)}\,(-1)^n(4\,n+3)\, \frac{P_{2\,n+1}(\cos\theta)}{r^{2\,n+2}} \ . $


Eduardo H. M. Brietzke